1) В урне находятся 9 белые, 11 черные, 8 желтые и 22 зеленных шаров. Какова вероятность того, что
вынутый шар будет а) белым; б) черным; в) желтым; г) зелёным?
2) Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях–будет
кратное число на 2?

Показать ответ

Ответ:

gg5765453232

12.05.2023 14:10

3.а)если х=2,то у=4•2+5=13

б)если х=6,то у=4•6+5=29

а)-6=-5х+4 б)19=-5х+4

-6-4=-5х 19-4=-5х

-10=-5х 15=-5х

х=2 х=-3

5.у=2х+b

(-3(x);5(y))

5=2•(-3)+b

5=-6+b

5+6=b

b=11

ответ:4)11Часть 2

1.Смотрите прикрепленный файл

2.у=-2х+3

А(3(x);9(y))

-2•3+3≠9

-3≠9

ответ:точка А не принадлежит графику у=-2х+3

B(4(x);-5(y))

-2•4+3=-5

-5=-5

ответ:точка B принадлежит графику у=-2х+3

3.А)нету фотографии графика

B)Смотрите прикрепленный файл

у=5-2х и у=3х-5

5-2х=3х-5

-2х-3х=-5-5

-5х=-10

х=2

у=5-2•2=1

ответ:(2;1)Графическим см.прикрепленный файл
3. Линейная функция задана формулой у = 4х + 5. Закончите решение: а) если х = 2, то у = ; б) если х

0,0(0 оценок)

Ответ:

Deniza06

03.12.2020 14:13

Есть формула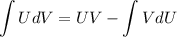 $\displaystyle \int UdV= UV - \int VdU$

Но напрямую я её использовать не очень люблю.

Проще использовать такой подход (он, конечно, на формуле основан)

1. "Разрезать" функцию на 2 части: одну, которую будем дифференцировать, а другую - интегрировать. Понятно, что это разбиение часто основывается на том, какую функцию проще интегрировать, так как продифференцировать можно любую (но иногда, как во 2-м примере, будем смотреть, какую функцию лучше дифференцировать).

2. В столбик написать обе получившиеся функции (ту, которую интегрируем, с дифференциалом запишем, естественно). Отчертить большой чертой и справа напротив каждой функции написать результат того, что мы с ней делаем (в одном случае результат интегрирования, а в другом дифференцирования).

3. А дальше итоговый интеграл будет равен "функция на функцию" (это будет крест накрест, где нет дифференциалов) минус интеграл от произведения функций справа.

Попробую на примере показать:

а) есть интеграл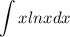 $\displaystyle \int x lnx dx$

Здесь удобнее интегрировать логарифм, а дифференцировать

$\displaystyle \left.\begin{matrix}lnx\\ xdx \end{matrix}\right| \begin{matrix}\frac{dx}{x}\\ \frac{x^2}{2} \end{matrix}$

Ну вот как-то так. И теперь сам интеграл:

$\displaystyle \int xlnxdx = \frac{x^2}{2}\cdot lnx-\int \frac{x^2}{2}\cdot \frac{1}{x}dx=\frac{x^2}{2}\cdot lnx-\int \frac{x}{2}dx=\\=\frac{x^2}{2}\cdot lnx-\frac{x^2}{4}+C$

Надеюсь, что стало понятнее.

б) здесь придется интеграл по частям брать аж 2 раза, но ничего страшного, возьмем.

Сам интеграл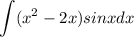 $\displaystyle \int(x^2-2x)sinxdx$

Здесь понятно, что тригонометрия будет давать тригонометрию что при интегрировании, что при дифференцировании, а вот многочлен уже при втором дифференцировании даст константу, так что его и будем дифференцировать.

$\displaystyle \left.\begin{matrix}x^2-2x\\ sinxdx \end{matrix}\right| \begin{matrix}(2x-2)dx\\ -cosx \end{matrix}$