1. Запишите формулу вероятности события с равновероятными исходами.
2. Запишите формулу числа перестановок из k элементов.
3. Сколькими можно выбрать трех дежурных из 25 учеников класса?
4. Сколькими можно выбрать 4 краски из 10 различных красок?
5. В соревнованиях по спортивной гимнастике участвуют 12 человек. Сколькими можно установить порядок их подхода к снаряду?
6. Сколько можно составить флагов с тремя горизонтальными полосами, если для окраски полос можно использовать 5 разных цветов, а все полосы на флаге различны по цвету?
7. Бросается одновременно две игральные кости. Какова вероятность, что сумма выпавших очков будет равна 10?
8. Бросают дважды игральную кость. Какова вероятность, что сумма набранных очков, будет равна 6?
9. Из карточной колоды в 36 карт наугад вынимают две карты. Какова вероятность, что обе карты окажутся тузами?
10. Из карточной колоды в 36 карт наугад вынимают две карты. Какова вероятность, что обе карты окажутся одной масти?
Четные числа отличаются друг от друга на 2; например, 4, 6 и 8 или 12, 14 и 16.
Пусть 1-е число - х, тогда 2-е число - (х + 2), а 3-е число - (х + 4). Составим и решим уравнение по условию задачи:
х² + (х + 2)² = (х + 4)²,
х² + х² + 4х + 4 = х² + 8х + 16,
2х² + 4х + 4 = х² + 8х + 16,
2х² + 4х + 4 - х² - 8х - 16 = 0,
х² - 4х - 12 = 0.
D = (-4)² - 4 · 1 · (-12) = 16 + 48 = 64; √64 = 8.
х₁ = (4 + 8) / (2 · 1) = 12 / 2 = 6, х₂ = (4 - 8) / (2 · 1) = -4 / 2 = -2.
Значит, три четных числа - это числа 6, 8 и 10 или -2, 0 и 2.
ответ: 6, 8 и 10 или -2, 0 и 2.
Для удобства для начала отдельно рассмотрю числитель
Заметим, что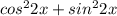 равно одному, это главное тригоном. тождество,
равно одному, это главное тригоном. тождество,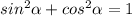 , только в нашем случае α=2x
, только в нашем случае α=2x
напомню, что
Заменяем на единицу и все упрощается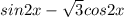
И так получили следущее
При этом
У нас получилось две серии корней, с периодами пи/2. поэтому на на круге будет очень много корней. Не знаю так знадумывалось ли, но придётся проверять знаки на промежутках между этими корнями. В итоге на круге будет 8 корней. Некоторая переодичность в знакопостоянстве улавливается, но не сразу и она не однозначна.
Нам нужно <0.
И выходит: