|x - 4| + |3y - 7| ≤ 0
По скольку |x - 4| ≥ 0 и |3y - 7| ≥ 0 ( |x| ≥ 0) , то |x - 4| + |3y - 7| ≥ 0
Значит :
|x - 4| + |3y - 7| = 0
[ x - 4 = 0 => x = 4
[ 3y - 7 = 0 => 3y = 7 => y = 7/3
x + y = 4 + 7/3 = 12/3 + 7/3 = 19/3
ответ : 19/3
Сумма двух положительных (или нулевых) чисел не может быть меньше 0.
Значит, единственный вариант: .
Это возможно только в том случае, если оба слагаемых = 0.
Значит - ответ.
================
Если решение удовлетворило, не забудь отметить его как "Лучшее".
|x - 4| + |3y - 7| ≤ 0
По скольку |x - 4| ≥ 0 и |3y - 7| ≥ 0 ( |x| ≥ 0) , то |x - 4| + |3y - 7| ≥ 0
Значит :
|x - 4| + |3y - 7| = 0
[ x - 4 = 0 => x = 4
[ 3y - 7 = 0 => 3y = 7 => y = 7/3
x + y = 4 + 7/3 = 12/3 + 7/3 = 19/3
ответ : 19/3
Сумма двух положительных (или нулевых) чисел не может быть меньше 0.
Значит, единственный вариант: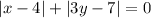
.
Это возможно только в том случае, если оба слагаемых = 0.
Значит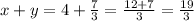
- ответ.
================
Если решение удовлетворило, не забудь отметить его как "Лучшее".