1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)
D>0 a>-25/16 a>-1,5625
Разбиваем ОДЗ на две части:
а) (-1; беск)
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
ответ: 1
y = x² - 3x + 2
Если график пересекает ось абсцисс , то ордината точки пересечения равна нулю, то есть y = 0. Найдём абсциссу точки пересечения :
0 = x² - 3x + 2
x² - 3x + 2 = 0
(x - 2)(x - 1) = 0
или x - 2 = 0 и тогда x = 2
или x - 1 = 0 и тогда x = 1
Нашли две точки пересечения графика с осью OX, координаты которых :
(2 ; 0) , (1 ; 0)
Если график пересекает ось ординат , то абсцисса точки пересечения равна нулю, то есть x = 0. Найдём ординату точки пересечения :
y = 0² - 3 * 0 + 2 = 2
Координаты точки пересечения с осью OY : (0 ; 2)
1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)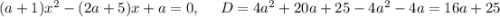
D>0 a>-25/16 a>-1,5625
Разбиваем ОДЗ на две части:
а) (-1; беск)
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49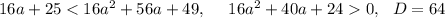
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
ответ: 1
y = x² - 3x + 2
Если график пересекает ось абсцисс , то ордината точки пересечения равна нулю, то есть y = 0. Найдём абсциссу точки пересечения :
0 = x² - 3x + 2
x² - 3x + 2 = 0
(x - 2)(x - 1) = 0
или x - 2 = 0 и тогда x = 2
или x - 1 = 0 и тогда x = 1
Нашли две точки пересечения графика с осью OX, координаты которых :
(2 ; 0) , (1 ; 0)
Если график пересекает ось ординат , то абсцисса точки пересечения равна нулю, то есть x = 0. Найдём ординату точки пересечения :
y = 0² - 3 * 0 + 2 = 2
Координаты точки пересечения с осью OY : (0 ; 2)