Попробуем составить функцию с таким графиком. Заметим, что функция имеет форму W, а значит модуль был применен два раза. Заметим, что "уголок" - это часть функции, отраженная относительно OX. Обозначим, нашу показанную функцию как F, на шаге до этого как f1. Тогда:
+2 - так как нижние уголки сдвинуты наверх на 2.
Теперь заметим, что высота уголка направленного вверх равна 3. Значит была некоторая функция f2 от которой взяли модуль опустили на 3 и получили f1. Запишем это:
Заметим, что f2 была функцией вида kx+b (примите как факт). Попробуем составить уравнение прямой, которая бы соответствовала рисунку:
k определяем по наклону левой части графика W. Решаем уравнение:
плотность распределения - это производная функции распределения. она равна 0 при х≤1, х>0; и равна
x-1/2 при 1<x≤2
Чтобы найти мат. ожидание. надо найти определенный интеграл от
х*f(dx) от 1 до двух. этот интеграл равен (х³/3-х²/4) от 1 до двух. По формуле Ньютона - Лейбница получаем 8/3-1-(1/3-1/4)=4/3-1/4=13/12
Квадрат мат. ожидания равен 169/144
а дисперсия есть определенный интеграл от 1 до двух от функции х²*f(dx) -М²(х)
интеграл равен х⁴/4-х³/6, подставляем пределы, получаем
4-4/3-(1/4-1/6)=8/3-1/12=31/12, отнимем теперь квадрат мат. ожидания от этой величины и получим дисперсию.
31/12-169/144=(31*12-169)/144=(372-169)/144=203/144=1 59/144
ответ: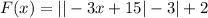
Объяснение:
Попробуем составить функцию с таким графиком. Заметим, что функция имеет форму W, а значит модуль был применен два раза. Заметим, что "уголок" - это часть функции, отраженная относительно OX. Обозначим, нашу показанную функцию как F, на шаге до этого как f1. Тогда:
+2 - так как нижние уголки сдвинуты наверх на 2.
Теперь заметим, что высота уголка направленного вверх равна 3. Значит была некоторая функция f2 от которой взяли модуль опустили на 3 и получили f1. Запишем это:
Заметим, что f2 была функцией вида kx+b (примите как факт). Попробуем составить уравнение прямой, которая бы соответствовала рисунку:
k определяем по наклону левой части графика W. Решаем уравнение:
Отсюда получаем функции: