букв 3, поэтому разделив полученное количество элементов на 3 получим количество С 610/3=203.3333 Округляем до ближайшего целого. 203.
В меньшую сторону округлили потому что судя по первым членам последовательность никогда не начинается с элемента С и быть его больше других в последовательности не может. Нечетные элементы начинаются с символа А, значит в 15 элементе также 204 B и 203A.
сначала решаем уравнение как и обычно т.е. Теоремой Виетта или Дискриминантом
х^2-4х+3=0
Я решу теоремой Виетта:
Сумма корней равна 4
Произведение 3
Значит корни 1 и 3
Далее:
Есть такая формула разложение на множетели квадратного уравнения выглядит так: a(x-x1)(x-x2), где а-множетель перед квадратом в нашем случае это 1, х1 и х2 - корни.
Подставим в неё наши корни, получим (x-1)(x-3)=0
Так а теперь решим это НЕРАВЕНСТВО (x-1)(x-3)>0
Методом интегралов ( тут 3 промежутка от минус бесконечности до 1 от 1 до 3 и от 3 до плюс бесконечности):
Допустим х =0, подставим (0-1)(0-3)=3 знак + значит в промежутке от минус бесконечности до 1 знак +
от 1 до 3 знак -
от 3 до плюс бесконечности +
ответ: х принадлежит промежутку от минус бесконечности до 1 и от 3 до плюс бесконечности
количество символов в первых элементах напоминает послдедовательность фиббоначи, которая задается следующим образом
x0=1
x1=1
x2=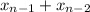
14 элемент твоей последовательности будет по количеству символов равен 15тому элементу последовательности фиббоначи, найдем его
x1=1; x2=2; x3=3; x4=5; x6=8; x7=13; x8=21; x9=34; x10=55; x11=89; x12=144; x13=233; x14= 377; x15=610.
в 15том члене последовательности 610 элементов.
букв 3, поэтому разделив полученное количество элементов на 3 получим количество С 610/3=203.3333 Округляем до ближайшего целого. 203.
В меньшую сторону округлили потому что судя по первым членам последовательность никогда не начинается с элемента С и быть его больше других в последовательности не может. Нечетные элементы начинаются с символа А, значит в 15 элементе также 204 B и 203A.
Получается делаем так:
сначала решаем уравнение как и обычно т.е. Теоремой Виетта или Дискриминантом
х^2-4х+3=0
Я решу теоремой Виетта:
Сумма корней равна 4
Произведение 3
Значит корни 1 и 3
Далее:
Есть такая формула разложение на множетели квадратного уравнения выглядит так: a(x-x1)(x-x2), где а-множетель перед квадратом в нашем случае это 1, х1 и х2 - корни.
Подставим в неё наши корни, получим (x-1)(x-3)=0
Так а теперь решим это НЕРАВЕНСТВО (x-1)(x-3)>0
Методом интегралов ( тут 3 промежутка от минус бесконечности до 1 от 1 до 3 и от 3 до плюс бесконечности):
Допустим х =0, подставим (0-1)(0-3)=3 знак + значит в промежутке от минус бесконечности до 1 знак +
от 1 до 3 знак -
от 3 до плюс бесконечности +
ответ: х принадлежит промежутку от минус бесконечности до 1 и от 3 до плюс бесконечности