Очень интересная задача! 1) Если x<0 U x>5, то 5x-x^2<0 Тогда |5x-x^2|=x^2-5x 5x^2-25x+10x^3+6 < x^4+25x^2 x^4-10x^3+20x^2+25x-6>0 Оно раскладывается на множители (x+1)(x-6)(x^2-5x+1)>0 Третья скобка > 0 при x<0 и при x>5. (x+1)(x-6)>0 x€(-oo;-1) U (6;+oo) 2) Если x€(0;5), то 5x-x^2>0 Тогда |5x-x^2|=5x-x^2 x^4-10x^3+30x^2-25x-6>0 Оно раскладывается так (x-2)(x-3)(x^2-5x-1)>0 Третья скобка <0 при x€(0,5) (x-2)(x-3)<0 x€(2; 3) ответ: x€(-oo;-1)U(2;3)U(6;+oo)
1) Если x<0 U x>5, то 5x-x^2<0
Тогда |5x-x^2|=x^2-5x
5x^2-25x+10x^3+6 < x^4+25x^2
x^4-10x^3+20x^2+25x-6>0
Оно раскладывается на множители
(x+1)(x-6)(x^2-5x+1)>0
Третья скобка > 0 при x<0 и при x>5.
(x+1)(x-6)>0
x€(-oo;-1) U (6;+oo)
2) Если x€(0;5), то 5x-x^2>0
Тогда |5x-x^2|=5x-x^2
x^4-10x^3+30x^2-25x-6>0
Оно раскладывается так
(x-2)(x-3)(x^2-5x-1)>0
Третья скобка <0 при x€(0,5)
(x-2)(x-3)<0
x€(2; 3)
ответ: x€(-oo;-1)U(2;3)U(6;+oo)
По виду графика. Например :
1) Прямая линия соответствует линейной функции y = kx + b.
k>0 ⇒ прямая наклонена вправо - функция возрастающая.
k<0 ⇒ прямая наклонена влево - функция убывающая.
k=0 ⇒ прямая параллельна оси ОХ.
b>0 ⇒ прямая пересекает ось OY выше оси OX.
b<0 ⇒ прямая пересекает ось OY ниже оси OX.
b=0 ⇒ прямая проходит через точку начала координат.
2) Парабола соответствует квадратичной функции y = ax² + bx + c
a>0 ⇒ ветви параболы направлены вверх.
a<0 ⇒ ветви параболы направлены вниз.
c>0 ⇒ парабола пересекает ось OY выше оси OX.
c<0 ⇒ парабола пересекает ось OY ниже оси OX.
c=0 ⇒ параболы проходит через точку начала координат.
3) Гипербола соответствует функции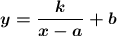
и состоит из двух частей.
4) Половинка лежащей параболы соответствует функции y =√x
Для установления соответствия можно проанализировать, в каких точках графики пересекают оси координат.