(см. объяснение)
Объяснение:
Заметим, что не является корнем уравнения.
Тогда поделим его на :
Выполним группировку:
Заметим, что если - корень уравнения, то тоже.
Тогда единственное решение возможно, если .
Иными словами, исходное уравнение может иметь ровно один корень тогда, когда .
Подставляя в исходное уравнение, получаем, что
Подставляя , получаем, что
Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.
Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.
Итого при исходное уравнение имеет единственное решение.
Задание выполнено!
(см. объяснение)
Объяснение:
Заметим, что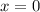 не является корнем уравнения.
не является корнем уравнения.
Тогда поделим его на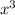 :
:
Выполним группировку:
Заметим, что если - корень уравнения, то
- корень уравнения, то  тоже.
тоже.
Тогда единственное решение возможно, если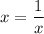 .
.
Иными словами, исходное уравнение может иметь ровно один корень тогда, когда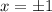 .
.
Подставляя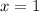 в исходное уравнение, получаем, что
в исходное уравнение, получаем, что 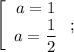
Подставляя , получаем, что
, получаем, что 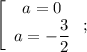
Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.
Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.
Итого при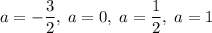 исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!