Пусть левая и правая часть равны у. Тогда получим систему:
Рассмотрим каждое уравнение как функцию.
- возрастающая функция, так как это кубическая парабола с положительным старшим коэффициентом
- убывающая функция, так как корень нечетной степени имеет сомножителем отрицательное число
Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.
В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.
Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.
Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.
Пусть , то есть . Проверим, является ли это число корнем:
- не корень
Пусть , то есть . Проверим, является ли это число корнем:
- не корень
Пусть , то есть . Проверим, является ли это число корнем:
- корень
Таким образом, уравнение имеет единственный корень
В планиметрии все фигуры, которые рассматривались при доказательстве каждой теоремы или при решении задач, располагались на плоскости (на листе бумаги или на доске и т. д.). Таким образом, мы имели дело только с одной плоскостью, и все точки, линии, углы, вообще геометрические фигуры лежали только на ней.
В курсе стереометрии нам предстоит рассматривать такие случаи, когда не все точки, линии и углы данной или данных фигур будут располагаться на одной плоскости. Будем считать, например, поверхность стола моделью плоскости Р; возьмем куб и поставим его одной гранью на стол. Легко видеть, что в данном кубе:
1) имеются точки, ребра, углы, лежащие на данной плоскости Р (на столе);
2) имеются точки, которые находятся вне плоскости Р;
3) имеются ребра, пересекающие плоскость Р;
4) имеются углы, находящиеся вне плоскости Р;
5) имеются шесть граней, являющиеся моделями шести различных плоскостей.
Вывод. Плоскости могут вступать во взаимодействие с другими элементами фигур и друг с другом.
Отсюда вытекает необходимость изучать различные случаи комбинаций плоскостей между собой, комбинации плоскостей с линиями и другими геометрическими объектами. Это изучение является одной из задач курса стереометрии. В первую очередь надо выяснить основные свойства плоскостей по отношению друг к другу, к точкам и прямым.
Запишем уравнение в виде:
Пусть левая и правая часть равны у. Тогда получим систему:
Рассмотрим каждое уравнение как функцию.
Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.
В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.
Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.
Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.
Пусть![\sqrt[3]{x-4} =\sqrt[3]{0}](/tpl/images/1360/1028/d91f8.png)
, то есть 
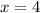. Проверим, является ли это число корнем:
Пусть![\sqrt[3]{x-4} =\sqrt[3]{1}](/tpl/images/1360/1028/7bd4a.png)
, то есть 
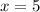. Проверим, является ли это число корнем:
Пусть![\sqrt[3]{x-4} =\sqrt[3]{-1}](/tpl/images/1360/1028/4572f.png)
, то есть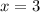 
. Проверим, является ли это число корнем:
Таким образом, уравнение имеет единственный корень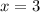
ответ: 3
В планиметрии все фигуры, которые рассматривались при доказательстве каждой теоремы или при решении задач, располагались на плоскости (на листе бумаги или на доске и т. д.). Таким образом, мы имели дело только с одной плоскостью, и все точки, линии, углы, вообще геометрические фигуры лежали только на ней.
В курсе стереометрии нам предстоит рассматривать такие случаи, когда не все точки, линии и углы данной или данных фигур будут располагаться на одной плоскости. Будем считать, например, поверхность стола моделью плоскости Р; возьмем куб и поставим его одной гранью на стол. Легко видеть, что в данном кубе:
1) имеются точки, ребра, углы, лежащие на данной плоскости Р (на столе);
2) имеются точки, которые находятся вне плоскости Р;
3) имеются ребра, пересекающие плоскость Р;
4) имеются углы, находящиеся вне плоскости Р;
5) имеются шесть граней, являющиеся моделями шести различных плоскостей.
Вывод. Плоскости могут вступать во взаимодействие с другими элементами фигур и друг с другом.
Отсюда вытекает необходимость изучать различные случаи комбинаций плоскостей между собой, комбинации плоскостей с линиями и другими геометрическими объектами. Это изучение является одной из задач курса стереометрии. В первую очередь надо выяснить основные свойства плоскостей по отношению друг к другу, к точкам и прямым.
Введем обозначения:
точки – А, В, С и т. д.
прямые – a, b, с и т. д. или (АВ, СD и т. д.)
плоскости – α, β, γ и т. д.