Данная функция является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию:
Для нахождения единственного экстремума воспользуемся производной:
По лемме Ферма, значение производной от экстремума нулевое. Таким образом, точки экстремума будет решением .
Для нахождения точки экстремума вычислим значение исходной функции от найденного :
2)Чтобы не выполняя построения найти точку пересечения графиков функции, необходимо решить систему, состояющую из двух уравнений этих функций, но т.к. у нас в обеих частях y, то т.к. равны левые части, равны и правые, а значит
5x+4=4x-7
x=-11. Подставим это значение в любую из двух функций, допустим во вторую, тогда
y=4*(-11)-7=-44-7=-51. Записывая координаты точек, изначально пишем икс, затем игрек, тогда точка пересечения имеет координаты (-11;-51),
3) все наши графики - прямые, а чтобы построить прямую, необходимо знать 2 произвольных точки. Пусть это будут точки 0 и 2(по иксу) для всех графиков, тогда в 1-ом при икс=0 игрек равен минус 4, а при икс=2, игрек равен -3. Отмечаем точки (0;-4) и (2;-3) на координатной плоскости, и проводим через них одну прямую, не забывая подписать ее график.
вторая прямая. х=0, у=4. х=2, у=3. Вообще, чтобы построить график этой функции, достаточно заметить, что это первая функция со знаком минус, но наверное для этого еще рано, отмечаем две точки с координатами (0;4) и (2;3) на координатной плоскости и проводим через них прямую, не забывая ее подписать.
Последняя прямая это биссектриса 2-го и 4-го квадранта, она строится, обычно без точек, но возьмем 0 и 2, тогда при х=0 у=0( начало координат) а при х=2, игрик равен -2, отмечаем точку (2;-2) на координатной плоскости и проводим по ней и началу координат прямую, не забывая ее подписать.
Объяснение:
Данная функция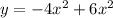 является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию: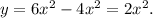
Для нахождения единственного экстремума воспользуемся производной:
единственного экстремума воспользуемся производной: 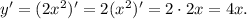
По лемме Ферма, значение производной от экстремума нулевое. Таким образом,
экстремума нулевое. Таким образом,  точки экстремума будет решением
точки экстремума будет решением 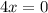 .
.
Для нахождения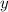 точки экстремума вычислим значение исходной функции от найденного
точки экстремума вычислим значение исходной функции от найденного  :
:
Получается, что координаты точки экстремума это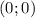 .
.
Объяснение:
1)Т.к. f(x)=20, при х=-4, то 20=3*(-4)+b
20=-12+b
b=20+12
b=32
2)Чтобы не выполняя построения найти точку пересечения графиков функции, необходимо решить систему, состояющую из двух уравнений этих функций, но т.к. у нас в обеих частях y, то т.к. равны левые части, равны и правые, а значит
5x+4=4x-7
x=-11. Подставим это значение в любую из двух функций, допустим во вторую, тогда
y=4*(-11)-7=-44-7=-51. Записывая координаты точек, изначально пишем икс, затем игрек, тогда точка пересечения имеет координаты (-11;-51),
3) все наши графики - прямые, а чтобы построить прямую, необходимо знать 2 произвольных точки. Пусть это будут точки 0 и 2(по иксу) для всех графиков, тогда в 1-ом при икс=0 игрек равен минус 4, а при икс=2, игрек равен -3. Отмечаем точки (0;-4) и (2;-3) на координатной плоскости, и проводим через них одну прямую, не забывая подписать ее график.
вторая прямая. х=0, у=4. х=2, у=3. Вообще, чтобы построить график этой функции, достаточно заметить, что это первая функция со знаком минус, но наверное для этого еще рано, отмечаем две точки с координатами (0;4) и (2;3) на координатной плоскости и проводим через них прямую, не забывая ее подписать.
Последняя прямая это биссектриса 2-го и 4-го квадранта, она строится, обычно без точек, но возьмем 0 и 2, тогда при х=0 у=0( начало координат) а при х=2, игрик равен -2, отмечаем точку (2;-2) на координатной плоскости и проводим по ней и началу координат прямую, не забывая ее подписать.
Выглядеть это будет так