Объяснение:
ab(a+b) (a+b)(-ab+)
(a+b)(ab-+ab-)0
-(a+b)(-2ab+)0
(a+b)0
Первый множитель 0 (по условию a≥0 b≥0), второй тоже 0 (квадрат). Значит и их произведение 0. ЧТД.
Объяснение:
ab(a+b)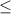 (a+b)(
(a+b)(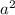 -ab+
-ab+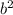 )
)
(a+b)(ab-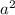 +ab-
+ab-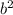 )
)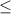 0
0
-(a+b)(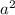 -2ab+
-2ab+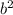 )
)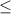 0
0
(a+b)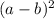
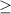 0
0
Первый множитель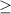 0 (по условию a≥0 b≥0), второй тоже
0 (по условию a≥0 b≥0), второй тоже 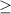 0 (квадрат). Значит и их произведение
0 (квадрат). Значит и их произведение 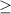 0. ЧТД.
0. ЧТД.