Объяснение:
сперва упорядочим все числа с минимального
чтобы найти среднее арифметическое число нужно прибавить все числа и разделить на количество (10)
Размах - для нахождения размаха надо от самого большого числа отнять малое
Найдём количество интервалов для таблицы - для этого размах должны разделить на 0,5
чтобы начать находить все интервалы нужно минимальное число отнять 0,1 дальше к полученому прибавляем 0,5
чтобы найти ni используем эти числа: 2 + 2 + 1 + 0 + 2 + 3 = 10
формула чтобы найти wi= так как n= 1, 2, 3, 4, 5, 6
w1 = 0.2
w2 = 0.2
w3 = 0.1
w4 = 0
w5 = 0.2
w6 = 0.3
чтобы расчитать xi нужно плюсовать каждый интервал и делить пополам
ответ есть на фото
34=34 верно
Одно число n, следующее за ним (n+1)
Разность квадратов двух последовательных натуральных чисел
(n+1)²-n²
(Из бо`льшего вычитаем меньшее, потому что по условию разности квадратов неотрицательны
Следующие два последовательных натуральных чисел это (n+2) и (n+3)
Разность квадратов следующих двух последовательных натуральных чисел
(n+3)²-(n+2)²
(Здесь тоже из бо`льшего вычитаем меньшее)
Сумма разностей квадратов по условию равна 34.
Уравнение
((n+1)²-n²) + ((n+3)²-(n+2)²)=34
(n²+2n+1-n²)+(n²+6n+9-n²-4n-4)=34
2n+1+2n+5=34
4n=28
n=7
7; 8 и 9;10
(10²-9²)+(8²-7²)=19+15
Объяснение:
сперва упорядочим все числа с минимального
чтобы найти среднее арифметическое число нужно прибавить все числа и разделить на количество (10)
Размах - для нахождения размаха надо от самого большого числа отнять малое
Найдём количество интервалов для таблицы - для этого размах должны разделить на 0,5
чтобы начать находить все интервалы нужно минимальное число отнять 0,1 дальше к полученому прибавляем 0,5
чтобы найти ni используем эти числа: 2 + 2 + 1 + 0 + 2 + 3 = 10
формула чтобы найти wi=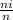 так как n= 1, 2, 3, 4, 5, 6
так как n= 1, 2, 3, 4, 5, 6
w1 = 0.2
w2 = 0.2
w3 = 0.1
w4 = 0
w5 = 0.2
w6 = 0.3
чтобы расчитать xi нужно плюсовать каждый интервал и делить пополам
ответ есть на фото
34=34 верно
Объяснение:
Одно число n, следующее за ним (n+1)
Разность квадратов двух последовательных натуральных чисел
(n+1)²-n²
(Из бо`льшего вычитаем меньшее, потому что по условию разности квадратов неотрицательны
Следующие два последовательных натуральных чисел это (n+2) и (n+3)
Разность квадратов следующих двух последовательных натуральных чисел
(n+3)²-(n+2)²
(Здесь тоже из бо`льшего вычитаем меньшее)
Сумма разностей квадратов по условию равна 34.
Уравнение
((n+1)²-n²) + ((n+3)²-(n+2)²)=34
(n²+2n+1-n²)+(n²+6n+9-n²-4n-4)=34
2n+1+2n+5=34
4n=28
n=7
7; 8 и 9;10
(10²-9²)+(8²-7²)=19+15