Алгебра: Arccos(-1/2)-2arctg под корнем 3+ arcctg 1/под корнем 3

Arccos(-1/2)-2arctg под корнем 3+ arcctg 1/под корнем 3

Показать ответ

Ответ:

Сашенька228

12.09.2022 10:37

а) Для определения вершины используем два уравнения. Для координаты по оси используем:

$\frac{-b}{2a} = \frac{1}{2} = 0,5$ .

Для координаты по оси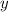 используем:

$-\frac{b^2-4ac}{4a} = -\frac{1+24}{4} = -\frac{25}{4} = -6,25$

Координата вершины параболы: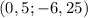 (0,5; -6,25)

б) График находится во всех четырёх четвертях, но преимущественно, конечно, в I и II четвертях.

в) Ось симметрии проходит через вершину параболы и параллельно оси ординат. На графике отображается синим цветом пунктирная линия. Ось симметрии проходит при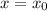 x = x_0 .

г) Пересечение с осью ординат: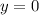 y = 0 при x = -2 и при x = 3

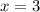
Пересечение с осью абсцисс: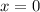 x = 0 при y = -6

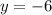
д) Во вложении график функции.

Дана функция y=х²-х-6а) Запиши координаты вершины параболы б)Определите в каких четвертях находятся

0,0(0 оценок)

Ответ:

DmitriyGromov

02.01.2023 21:56

$\begin{cases} 
& \text{ } x+y+z=0 \\ 
& \text{ } xy+yz=-1 \\
& \text{ } x^2+y^2+z^2=6
\end{cases}\Rightarrow\begin{cases} 
& \text{ } x+z=-y \\ 
& \text{ } y(x+z)=-1 \\
& \text{ } x^2+y^2+z^2=6
\end{cases}$
Первое уравнение подставим во второе, тоесть:
$\begin{cases} 
& \text{ } x+z=-y \\ 
& \text{ } y\cdot(-y)=-1 \\
& \text{ } x^2+y^2+z^2=6
\end{cases}\Rightarrow\begin{cases} 
& \text{ } x+z=-y \\ 
& \text{ } y^2=1 \\
& \text{ } x^2+y^2+z^2=6
\end{cases}$

Второе уравнение можно решить без проблем:
   $y^2=1\\ y=\pm 1$

Тоесть, мы будем иметь 2 системы с двумя уравнения:
  1 система уравнения
Если y=1;.
   $\begin{cases} 
& \text{ } x+z=-1 \\ 
& \text{ } x^2+z^2=5 
\end{cases}$
Из первого уравнения выразим переменную х, и подставим во второе уравнение
$\begin{cases} 
& \text{ } x=-1-z \\ 
& \text{ } (-1-z)^2+z^2=5 
\end{cases}$
Раскрываем скобки и приводим подобные слагаемые.
$1+2z+z^2+z^2-5=0\\ 2z^2+2z-4=0|:2\\ z^2+z-2=0$
Получили квадратное уравнение. По теореме Виета, мы можем найти корни: $z_1=-2;\,\,\,\, z_2=1$
Находим теперь переменны

$x_1=-1-z_1=-1+2=1\\ x_2=-1-z_2=-1-1=-2$

2 система уравнения.
Если y=-1

$\begin{cases} 
& \text{ } x+z=1 \\ 
& \text{ } x^2+z^2=5 
\end{cases}$
Из первого уравнения выразим переменную х и подставим во второе уравнение
$\begin{cases} 
& \text{ } x=1-z \\ 
& \text{ } (1-z)^2+z^2=5 
\end{cases}\\ 1-2z+z^2+z^2-5=0\\ \\ 2z^2-2z-4=0|:2\\ z^2-z-2=0$
По т. Виета:

$z_1=-1;\,\,\,\, z_2=2$

Находим переменные