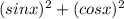Арифметикалық прогрессияның алғашқы екі мүшесі берілгеня: 30,24, а)прогрессияның оң мүшелерін санын анықтаңыз. b)қосындысы 78-ге тең болатын осы прогрессияның тізбектелген мүшелердің санын анықтаныз
Построим единичную окружность от начала координат, то есть радиус будет равен единице, и любой радиус-вектор соответственно. Построим треугольник, такой, что его гипотенуза - радиус. один из катетов лежит на оси абсцисс, а другой параллелен оси ординат. Тогда длина противолежащего катета равна координате y точки окружности, находящейся на радиусе, а длина прилежащего - координате x . Угол между гипотенузой и осью абсцисс обозначим за α. Как известно, синусом называется отношение противолежащего катета к гипотенузе, а косинусом называется отношение прилежащего катета к гипотенузе. Как уже было сказано, противолежащий катет равен y, а прилежащий равен x. Тогда sinα = y/1 (гипотенуза равна единице) = y, а cosα = x/1 = x. чтд
Очевидно, что если радиус - любое число, кроме единицы - равенства не будет.
Другой менее правильный. Известная формула расстояния между двумя точками:
d =
где x1, y1 - соответствующие координаты первой точки, x2,y2 - координаты второй точки.
На самом деле, это всего лишь теорема Пифагора, здесь d - гипотенуза прямоугольного треугольника, а если вычесть из кооординаты начала (x1 или y1) координату конца (x2 или y2), получится длина катета. Квадрат суммы длин катетов равен квадрату длины гипотенузы. Это работает для любых двух точек. Но синус и косинус равны координатам точки только на единичной окружности.
Если одна из точек будет лежать на краю окружности, а вторая будет началом координат, то x2 = y2 = 0, и тогда формула будет иметь другой вид:
d =
Нетрудно догадаться, что расстояние от центра окружности до ее края называется радиусом. В данном случае радиус равен 1, поэтому:
1 =
Это уравнение можно возвести в квадрат, так как обе его части неотрицательны:
1 =
Здесь, очевидно, спряталось основное тригонометрическое тождество. 1 =
Объяснение:
https://tex.z-dn.net/?f=%20%5Csqrt%7B11-4%20%5Csqrt%7B7%7D%7D%2B%20%5Csqrt%7B16-6%20%5Csqrt%7B7%7D%7D%3D%20%5Csqrt%7B7-2%2A2%20%5Csqrt%7B7%7D%2B4%7D%2B%5Csqrt%7B9-2%2A3%2A%5Csqrt%7B7%7D%2B7%7D%3D%20%5C%5C%20%3D%5Csqrt%7B%28%5Csqrt%7B7%7D%29%5E2-2%2A2%20%5Csqrt%7B7%7D%2B2%5E2%7D%2B%5Csqrt%7B3%5E2-2%2A3%2A%5Csqrt%7B7%7D%2B%28%5Csqrt%7B7%7D%29%5E2%7D%3D%20%5C%5C%20%3D%5Csqrt%7B%28%5Csqrt%7B7%7D-2%29%5E2%7D%2B%5Csqrt%7B%283-%20%5Csqrt%7B7%7D%29%5E2%7D%3D%7C%5Csqrt%7B7%7D-2%7C%2B%7C3-%20%5Csqrt%7B7%7D%7C%3D%20%5C%5C%20%3D%5Csqrt%7B7%7D-2%2B3-%20%5Csqrt%7B7%7D%3D1
Это ссылка!
Построим единичную окружность от начала координат, то есть радиус будет равен единице, и любой радиус-вектор соответственно. Построим треугольник, такой, что его гипотенуза - радиус. один из катетов лежит на оси абсцисс, а другой параллелен оси ординат. Тогда длина противолежащего катета равна координате y точки окружности, находящейся на радиусе, а длина прилежащего - координате x . Угол между гипотенузой и осью абсцисс обозначим за α. Как известно, синусом называется отношение противолежащего катета к гипотенузе, а косинусом называется отношение прилежащего катета к гипотенузе. Как уже было сказано, противолежащий катет равен y, а прилежащий равен x. Тогда sinα = y/1 (гипотенуза равна единице) = y, а cosα = x/1 = x. чтд
Очевидно, что если радиус - любое число, кроме единицы - равенства не будет.
Другой менее правильный. Известная формула расстояния между двумя точками:
d =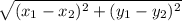
где x1, y1 - соответствующие координаты первой точки, x2,y2 - координаты второй точки.
На самом деле, это всего лишь теорема Пифагора, здесь d - гипотенуза прямоугольного треугольника, а если вычесть из кооординаты начала (x1 или y1) координату конца (x2 или y2), получится длина катета. Квадрат суммы длин катетов равен квадрату длины гипотенузы. Это работает для любых двух точек. Но синус и косинус равны координатам точки только на единичной окружности.
Если одна из точек будет лежать на краю окружности, а вторая будет началом координат, то x2 = y2 = 0, и тогда формула будет иметь другой вид:
d =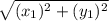
Нетрудно догадаться, что расстояние от центра окружности до ее края называется радиусом. В данном случае радиус равен 1, поэтому:
1 =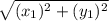
Это уравнение можно возвести в квадрат, так как обе его части неотрицательны:
1 =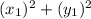
Здесь, очевидно, спряталось основное тригонометрическое тождество. 1 =