ответ: x = -π/4 + πn; x = 3π/4 - arcsin() + πn, n ∈ Z
Объяснение:
0,5sin(2x) + 7cos^2(x) - 3,5 + 3,5 = 3
0,5sin(2x) + 3,5cos(2x) = -0,5
sin(2x) + 7cos(2x) = -1
Разделим обе части на
Получаем:
Пусть sin(α) = , тогда cos(α) =
α = arcsin()
Получаем уравнение sin(2x)*cos(α) + sin(α)*cos(2x) = -cos(α)
Применяем формулы синуса суммы и формулу приведения
sin(2x + α) = -sin(π/2 - α)
sin(2x + α) = sin(α - π/2)
1) 2x + α = α - π/2 + 2πn
x = -π/4 + πn, n ∈ Z
2) 2x + α = π + π/2 - α + 2πn
x = 3π/4 - α + πn
x = 3π/4 - arcsin() + πn, n ∈ Z
ответ: x = -π/4 + πn; x = 3π/4 - arcsin(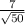 ) + πn, n ∈ Z
) + πn, n ∈ Z
Объяснение:
0,5sin(2x) + 7cos^2(x) - 3,5 + 3,5 = 3
0,5sin(2x) + 3,5cos(2x) = -0,5
sin(2x) + 7cos(2x) = -1
Разделим обе части на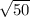
Получаем:
Пусть sin(α) =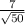 , тогда cos(α) =
, тогда cos(α) = 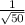
α = arcsin(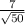 )
)
Получаем уравнение sin(2x)*cos(α) + sin(α)*cos(2x) = -cos(α)
Применяем формулы синуса суммы и формулу приведения
sin(2x + α) = -sin(π/2 - α)
sin(2x + α) = sin(α - π/2)
1) 2x + α = α - π/2 + 2πn
x = -π/4 + πn, n ∈ Z
2) 2x + α = π + π/2 - α + 2πn
x = 3π/4 - α + πn
x = 3π/4 - arcsin(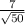 ) + πn, n ∈ Z
) + πn, n ∈ Z