в) Преобразуем числитель. (1-cos²x+sin²x)/(x*tg3x)=2sin²x/(x*tg3x), подведем данную запись под первый замечательный предел. При икс, стремящемся к нулю, sinx ; tg3x эквивалентны х и 3х соответственно, а потому получим предел дроби 2*х*х/(х*3х) и он равен 2/3.
2.
Общее число партий сыгранных между англичанами и немцами, французами и немцами, англичанами и французами можно найти двумя
Пусть число французов -
Число англичан -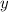
Число немцев -
Число партий вида: англичане - немцы
Число партий вида: англичане- французы
Число партий вида: немцы - французы
Таким образом :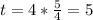
ответ: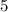
1.
Это уравнение можно переписать в виде:
Где: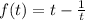
Нетрудно убедиться, что при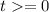
(радикалы неотрицательны) данная функция монотонно возрастет.
Действительно, ведь производная данной функции положительна.
А поскольку функция монотонна, то одинаковые значения функции могут быть только у одинаковых значений аргумента.
То есть из уравнения:
Следует равносильное ему уравнение:
ответ: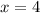
в) Преобразуем числитель. (1-cos²x+sin²x)/(x*tg3x)=2sin²x/(x*tg3x), подведем данную запись под первый замечательный предел. При икс, стремящемся к нулю, sinx ; tg3x эквивалентны х и 3х соответственно, а потому получим предел дроби 2*х*х/(х*3х) и он равен 2/3.
ответ 2/3
г) преобразуем (4-x)*(㏑(2-3х)-㏑(5-3х))=(4-x)*(㏑((2-3х)/(5-3х))=
(4-x)㏑((3х-2)/(3х-5))=(4-x)㏑((1+3/(3x-5))=㏑((1+3/(3x-5))^(4-x)
cвели решение ко второму замечательному пределу, возьмем сначала предел от (1+3/(3x-5))^(4-x), а затем логарифм от полученного предела.
представим (1+3/(3x-5))⁽⁴ ⁻ˣ⁾=(((1+(3/(3x-5)))⁽³ˣ ⁻⁵⁾/³))⁽³⁽⁽⁴⁻ˣ⁾/⁽³ ˣ⁻⁵)предел от этого выражения равен е⁻¹, а ㏑е⁻¹=-1*lnе=-1
ответ -1