Чтобы сделать заказ вовремя, бригада рабочих должна укладывать в день по 12 кв. м плитки. Но рабочие укладывали на 2 кв. м больше и выполнили заказ на 3 дня раньше. Каков был срок исполнения заказа?
1) угловой коэффициент k=-0,7 2) х=2у+2 2у=х-2 у=х/2-1 Угловой коэфф. к=1/2 3) -5х+3у+16=0 3у=5х-16 у=5х/3-16/3 Угловой коэфф. k=5/3 № 3. 1) (х-3)²+(у-1)²=9 (х-3)²+(у-1)²=3² Графиком будет окружность с радиусом 3 с центром в точке с координатами (3; 1) 2) у=(х-2)²-1 у=х²-4х+4-1 у=х²-4х+3 График функции - парабола, ветви направлены вверх ( а>0) Нули функции х1=1 и х2=3. (Точки пересечения с осью ОХ) При х =0, у=3 - точка пересечения с осью ОУ 3) у=х²-2 График - парабола ветвями вверх. При х=0, у=-2.
2) х=2у+2
2у=х-2
у=х/2-1 Угловой коэфф. к=1/2
3) -5х+3у+16=0
3у=5х-16
у=5х/3-16/3 Угловой коэфф. k=5/3
№ 3.
1) (х-3)²+(у-1)²=9
(х-3)²+(у-1)²=3² Графиком будет окружность с радиусом 3 с центром в точке с координатами (3; 1)
2) у=(х-2)²-1 у=х²-4х+4-1 у=х²-4х+3
График функции - парабола, ветви направлены вверх ( а>0) Нули функции х1=1 и х2=3. (Точки пересечения с осью ОХ)
При х =0, у=3 - точка пересечения с осью ОУ
3) у=х²-2
График - парабола ветвями вверх. При х=0, у=-2.
1. Обратно пропорциональная зависимость :
2. Решите графически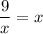
График функции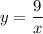 - гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение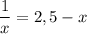
График функции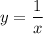 - гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.