Y=sinx 1.Обл. определения D(f) = (-бесконечности; +бесконечности) или R - множество действительных чисел 2.Обл. значения E(f) = [-1;1] 3. y возрастает при x Є [-π/2 + 2πn; π/2 + 2πn] n Є Z(целые числа) y убывает при x Є [π/2 + 2πn; 3π/2 + 2πn] n Є Z(целые числа) 4. Функция нечетная (симметрична относительно началу координат) sin(-x) = -sinx 5. Период T=2π
y=cosx 1. D(f) = R 2. E(f) = [-1:1] 3. у возрастает при x Є [-π + 2πn; 2πn] у убывает при x Є [2πn; π + 2πn] 4. Функция четная (симметрична относительно оси OY) 5. T=2π
Вариант 2.
Задание 1.
1.
х = 18 :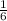
х = 18 * 6
х = 108
2.
7х + 11,9 = 0
7х = -11,9
х = -11,9 : 7
х = -1,7
3.
6х - 0,8 = 3х + 2,2
6х - 3х = 2,2 + 0,8
3х = 3
х = 3 : 3
х = 1
4.
5х - (7х + 7) = 9
5х - 7х - 7 = 9
-2х = 9 + 7
-2х = 16
х = 16 : (-2)
х = -8
Задание 2.
х км - на автобусе
9х км - на самолете
Составляем уравнение:
х + 9х = 600
10х = 600
х = 600 : 10
х = 60
60 км - на автобусе .
ответ: 60 км.
Задание 3.
Допустим на другом участке было х саженцев, тогда на первом - 5х .
После перевоза получилось:
х + 90 - другой участок.
5х - 50 - первый участок.
Составляем уравнение:
5х - 50 = х + 90
5х - х = 90 + 50
4х = 140
х = 140:4
х = 35
35 саженцев - на другом участке первоначально.
35 * 5 = 175 саженцев - было на первом участке первоначально.
ответ: 175, 35.
Задание 4.
6х - (2х - 5) = 2(2х + 4)
6х - 2х + 5 = 4х + 8
6х - 2х - 4х = 8 - 5
0х = 3
Нет решения.
1.Обл. определения D(f) = (-бесконечности; +бесконечности) или R - множество действительных чисел
2.Обл. значения E(f) = [-1;1]
3. y возрастает при x Є [-π/2 + 2πn; π/2 + 2πn] n Є Z(целые числа)
y убывает при x Є [π/2 + 2πn; 3π/2 + 2πn] n Є Z(целые числа)
4. Функция нечетная (симметрична относительно началу координат)
sin(-x) = -sinx
5. Период T=2π
y=cosx
1. D(f) = R
2. E(f) = [-1:1]
3. у возрастает при x Є [-π + 2πn; 2πn]
у убывает при x Є [2πn; π + 2πn]
4. Функция четная (симметрична относительно оси OY)
5. T=2π