Заметим, что график функции будет пересекать ось абсцисс и ось ординат в точке (это несложно определить, решив два уравнения и ), а также определен при всех значениях действительных значения аргумента .
Теперь можем определить несколько дополнительных точек (при желании, это можно было сделать и сразу):
Далее проводим через все эти точки плавную линию, как показано на чертеже в приложении.
График построен!
2 )
Функция четная или нечетная?
По построенному только что графику видно, что он симметричен относительно начала координат. Это означает, что рассматриваемая функция - нечетная (ведь если график симметричен относительно начала координат, то функция нечетная, а если симметричен относительно оси абсцисс, то нечетная).
Это можно было определить и аналитически. Как известно, если , то функция четная, а если , то нечетная (в противном случае функция свойством четности не обладает).
а⁴ + b⁴ ≥ а³b + аb³
1)
а⁴ + b⁴ - а³b - аb³ ≥ 0
а³(а-b) - b³(а-b) ≥ 0
(а-b)(а³-b³) ≥0
(а-b)(а-b)(а²+аb+b²) ≥0
(а-b)²·(а²+аb+b²) ≥0
2)
Первая скобка всегда больше или равна 0, остаётся доказать, что вторая скобка тоже всегда больше или равна 0.
а²+аb+b² ≥0
a) Докажем для неотрицательных a и b.
(a²+ab+ab+b²)-ab ≥ 0
(a² + 2ab + b²) ≥ ab
(a+b)² ≥ ab
а+b ≥ √аb
Это неравенство справедливо как следствие из теоремы Коши для среднего арифметического и среднего геометрического:
(а+b)/2 ≥ √аb
Таким образом, всегда справедливо неравенство во второй скобке
(a²+ab+b²) ≥ 0.
2) Докажем справедливость неравенства (a²+ab+b²) > 0 для отрицательных значений a и b.
a<0; b<0
a²>0; b²>0 - первое и третье слагаемые a² и b² всегда положительны
ab>0, как произведение двух отрицательных(минус × минус = плюс)
Сумма положительных слагаемых тоже положительна:
(a²+ab+b²) > 0
3) Докажем справедливость неравенства (a²+ab+b²) > 0 для значений a и b, различных по знаку: a>0; b<0.
(a²+ab+ab+b²)-ab > 0
(a² + 2ab + b²) > ab
(a+b)² > ab
Это неравенство справедливо, т.к.
(a+b)² ≥ 0
ab < 0 (плюс × минус = минус)
Положительное число больше отрицательного.
Таким образом все три варианта доказывают справедливость неравенства
(а²+ab+b²)≥0. Что и требовалось доказать.
Построим график функции y = x³.
Заметим, что график функции будет пересекать ось абсцисс и ось ординат в точке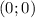 (это несложно определить, решив два уравнения
(это несложно определить, решив два уравнения 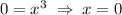 и
и 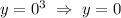 ), а также определен при всех значениях действительных значения аргумента
), а также определен при всех значениях действительных значения аргумента 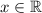 .
.
Теперь можем определить несколько дополнительных точек (при желании, это можно было сделать и сразу):
Далее проводим через все эти точки плавную линию, как показано на чертеже в приложении.
График построен!
2 )Функция четная или нечетная?
По построенному только что графику видно, что он симметричен относительно начала координат. Это означает, что рассматриваемая функция - нечетная (ведь если график симметричен относительно начала координат, то функция нечетная, а если симметричен относительно оси абсцисс, то нечетная).
Это можно было определить и аналитически. Как известно, если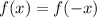 , то функция четная, а если
, то функция четная, а если 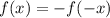 , то нечетная (в противном случае функция свойством четности не обладает).
, то нечетная (в противном случае функция свойством четности не обладает).
При этом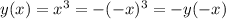 .
.
Так или иначе, получаем, что функция нечетная.
3 )Принадлежат ли точки графику?
а)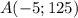 . НЕ принадлежит.
. НЕ принадлежит.
б)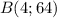 . Принадлежит.
. Принадлежит.
в)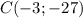 . Принадлежит.
. Принадлежит.
То есть графику принадлежат только точки B и C.