Детская площадка имеет форму прямоугольника, площадь которого равна 192 м2. Одна его сторона на 4 метр(-ов, -а) больше, чем другая. Детской площадке необходимо построить бордюр. В магазине продаётся материал для бордюра в упаковках. В одной упаковке имеется 25 метров(-а) материала.
1. Вычисли длину и ширину детской площадки.
Меньшая сторона детской площадки (целое число) равна:
м.
Большая сторона детской площадки (целое число) равна:
м.
2. Вычисли, сколько упаковок материала для бордюра необходимо купить.
Необходимое количество упаковок равно:
.
S = 5(15+2x)
Объяснение:
В решении задачи используем очень сложную формулу (шучу):
2 тела (автомобиля) выехали из одной точки в противоположные стороны.
Первый автомобиль преодолел за 5 часов S1=U1*t, или S1 =5x (потому что х - скорость первого автомобиля, а требуемое время - 5 часов (S1 - расстояние, которое преодолел первый автомобиль, а U1 - скорость первого автомобиля))
Второй автомобиль преодолел за 5 часов S2=U2*t, или S2 =5(x+15) (потому что скорость первого автомобиля на 15 больше первого, у первого - х, значит у второго - 15+х, а требуемое время - 5 часов (S2 - расстояние, которое преодолел второй автомобиль, а U2 - скорость второго автомобиля))
Складываем получившиеся выражения:
S = S1 + S2 = 5x + 5(x+15) = 5(x+15+x) = 5(15+2x)
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,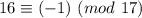 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что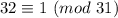 , получаем
, получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.