Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).
Это координаты вершины, почему именно такие? Корни уравнения:
, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.
Найдём нули функции:
Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.
И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: то есть (0;3)
1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения
При x∈(-1;3) функция принимает положительные значения
2) При x∈(-∞;1) функция растёт
При x∈(1;+∞) функция убывает
3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)
Максимальное значение 4, достигается в точке (1;4)
если меняется только одна цифра, значит, меняется только один разряд числа: единицы, десятки, сотни и т.д.
• Изменяя только единицы, деление на 18 снова не получится. Потому что от одного числа, которое делится на 18, до другого должна быть разница хотя бы в эти самые 18.
• Изменяя десятки, мы делаем предположение, что какое-либо круглое двузначное число делится на 18, и это так:
90 : 18 = 5.
Таким образом, если найдётся число, у которого в разряде десятков стоит 0, и оно делится на 18, достаточно будет заменить 0 на 9, чтобы получить новое число, делящееся на 18.
Пример: 108 и 198.
Для числа 19 ответ: нет, нельзя.
Рассуждения аналогичные, только в десятках умножение 19 ни на какое число не даст круглого двузначного числа. То же самое и с сотнями, и с тысячами и т.п., ведь из девятки на конце может получиться нуль только умножением на 10, или кратное ему, а это нам не подходит, т.к. числа 190 и подобные ему будут изменять не один разряд числа, а несколько. Так что только одну цифру изменить никак не получится.
Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).
Это координаты вершины, почему именно такие? Корни уравнения:
Найдём нули функции:
Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.
И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: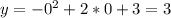
то есть (0;3)
1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения
При x∈(-1;3) функция принимает положительные значения
2) При x∈(-∞;1) функция растёт
При x∈(1;+∞) функция убывает
3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)
Максимальное значение 4, достигается в точке (1;4)
Для числа 18 ответ: да, можно.
Я рассуждал так:
если меняется только одна цифра, значит, меняется только один разряд числа: единицы, десятки, сотни и т.д.
• Изменяя только единицы, деление на 18 снова не получится. Потому что от одного числа, которое делится на 18, до другого должна быть разница хотя бы в эти самые 18.
• Изменяя десятки, мы делаем предположение, что какое-либо круглое двузначное число делится на 18, и это так:
90 : 18 = 5.
Таким образом, если найдётся число, у которого в разряде десятков стоит 0, и оно делится на 18, достаточно будет заменить 0 на 9, чтобы получить новое число, делящееся на 18.
Пример: 108 и 198.
Для числа 19 ответ: нет, нельзя.
Рассуждения аналогичные, только в десятках умножение 19 ни на какое число не даст круглого двузначного числа. То же самое и с сотнями, и с тысячами и т.п., ведь из девятки на конце может получиться нуль только умножением на 10, или кратное ему, а это нам не подходит, т.к. числа 190 и подобные ему будут изменять не один разряд числа, а несколько. Так что только одну цифру изменить никак не получится.