Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
afinaty4
30.04.2023 23:41 •
Алгебра
Для функции f(x)3x-6,написать первообразную график которой проходит через точку А(-2,-3)
Показать ответ
Ответ:
Аделина2201
18.10.2021 19:10
Объяснение:
Первообразная:
Так как
проходит через точку
то:
0,0
(0 оценок)
Популярные вопросы: Алгебра
amozgaleva96
05.07.2022 07:19
Задано функцію 3x-x, якщо x ≤4, y= x|2-3, якщо x 4.1) Побудуйте графік цієї функції.2) Визначте за графіком, при яких зна-ченнях аргумента функція набуваєвід ємних значень....
slava531
21.08.2021 23:32
Приведите пример двух рациональных чисел...
fearsomehusky
01.02.2021 03:57
Решить уравнение: 2*(25^x)-5*(4^x)=3*(10^x) 2. Сравните с числом 1 положительное число а, если a^Минус корень с 7 а^1.2 С объяснением...
nastyzotova12378
17.10.2022 15:20
(-8)⁵⁰÷(-8)³⁰= (3/14)³÷(3/14)²=...
Ира21fu
24.07.2022 15:04
Знайдіть найбільше значення виразу : 1-a² , -4 - a²...
dedrina
18.03.2021 06:33
(p^1-^n)^9:(p^2n+1)^4^- степень...
SergeGu
07.08.2022 14:45
Найдите корень уравнения: log 3(4-x)=9....
SeetFatRed819
07.08.2022 14:45
Втреугольнике abc ac=bc,ab=10; cos a = 5_13 ,найдите высоту сн...
кукипро
07.08.2022 14:45
Кенгуру прыгнуть в длину на 1 сантикилометр. сколько метров составляет длина такого прыжка? и вот ещё чё такое пунктов за решение? я не знаю что это и поставил 10...
Кристина01012004
07.08.2022 14:45
Является ли число 39 членом арифметической прогрессии(сn), в которой с1=-6 и с6=6?...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Объяснение:
Первообразная: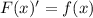
Так как проходит через точку
проходит через точку 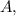 то:
то: