.Для каждого неравенства укажите множество его решений.
А) 9– х2> 0. Б) 9+ x2 > 0. В) 9– x2< 0.Г) 9+ х2< 0

1) ( - ∞; -3) ∪( 3; + ∞). 2) ( - ∞ ; + ∞ ). 3) ( -3; 3 ). 4) ( 3; + ∞ ) 5) ∅ 6) ( - ∞; -3)

обозначим угол наклона бокового ребра к основанию ß

по апофеме b посчитаешь площадь основания So и высоту H пирамиды по ф-ле

H=sinß*b

проекция b на основание b"=1/3*m=√(b^2-H^2)

половина стороны основания a/2=b"/tg60=√(b^2-H^2)/tg60

a=2*√(b^2-H^2)/√3

площадь основания So =a^2*√3/4 =(2*√(b^2-H^2)/√3 )^2*√3/4

объем пирамиды V =1/3*So*H =1/3*(2*√(b^2-H^2)/√3 )^2*√3/4 *sinß*b=

=1/3*(2*√(b^2-(sinß*b)^2)/√3 )^2*√3/4 *sinß*b

объем пирамиды меняется в зависимости от sinß

sinß - меняется от 0 до 1 , рассмотри значения sinß в этом интервале

найдешь наибольший возможный объём

1) Не буду переписывать всю систему, начну с решения.

выразим через второе уравнение  y:

y=2-5x

подставим y в первое уравнение:

2x-3(2-5x)=11

2x-6+15x=11

17x=17

x=1

Найдем y:

y=2-5*1=-3

ответ: (1;-3).

2) Решим первое неравенство:

 1-6x<10

6x>-9

x>-9/6

x>-1,5    - это решение первого неравенства.

 Решим второе неравенство:

 5x-7<x-7

4x<0

x<0  - это решение втрого неравенства.

 Общая часть интервалов (-1,5; +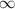) и (-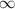;0) является промежуток (-1,5;0).

ответ:   (-1,5;0).