Добуток третього і дев'ятого елементів геометричної прогресії дорівнює 49, а п'ятий елемент цієї прогресії дорівнює 14.
Знайдіть знаменник прогресії, якщо всі її елементи додатні.
Произведение третьего и девятого элементов геометрической прогрессии равна 49, а пятый элемент этой прогрессии равна 14.
Найдите знаменатель прогрессии, если все ее элементы положительные.
Известно, что график проходит через точку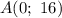 . Подставим значения в функцию и посмотрим, что получится.
. Подставим значения в функцию и посмотрим, что получится.
Итак, мы нашли свободный член. Теперь, используя две другие точки, можно найти старший и второй коэффициенты. Для этого нужно решить систему из двух уравнений. Она составляется очень просто: в общий вид квадратичной функции подставляются абсцисса и ордината этих точек.
Воспользуемся методом сложения и сложим верхнее уравнение с нижним.
Теперь подставим полученное значение в любое из уравнений системы, к примеру верхнее.
Итак, искомая аналитическая формула: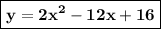 .
.
62. 7см, 14см, 10см
67. 7 девочек - в тренажерный зал
12 девочек - на шейпинг
14 девочек -на аквааэробику
69.
15 км/ч и 12 км/ч
62. Пусть х- меньшая сторона треугольника, тогда 2х- вторая сторона треугольника и (х+3)- третья сторона треугольника
х+2х+х+3=31 ;
4х=31-3;
х=28:4;
х=7( см)- 1 сторона
2х=2*7=14(см)- вторая сторона
х+3=7+3=10(см) - третья сторона
67.
Пусть в тренаженый зал ходит х старшекласниц, тогда (х+5) старшекласниц ходят на шейпинг и 2х- на аквааэробику.
По условию задачи составим уравнение:
х+х+5+2х=33;
4х=33-5;
х=28:4;
х=7 (ст.) - в тренажерный зал
х+5=7+5=12 (ст.) - на шейпинг
2*7=14 ( ст.) -на аквааэробику
69. Пусть х - скорость второго велосипедиста, а (х+3) - скорость первого. Тогда (х+х+3)- совместная скорость, с которой оба проехали путь до встречи за 40 минут
40минут=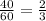 часа
часа
18=(х+х+3)*2/3;
2х+3=18*3/2;
2х=27-3;
х=24:2;
х=12 (км/ч)- скорость второго велосипедиста
х+3=12+3=15(км/ч)- скорость первого велосипедиста