1) База индукции: n = 1
- выполнено
2) Предположим что и для выражение
3) Индукционный переход:
Первое слагаемое делится на 5 по предположению (пункт 2). Остальные слагаемые тоже делятся на 5, поскольку их коэффициенты делятся на 5. Значит, исходное выражение кратно 5 для всех натуральных n.
1) База индукции: n = 1
2) Предположим что и для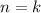
выражение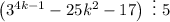 
3) Индукционный переход: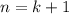
Первое слагаемое делится на 5 по предположению (пункт 2). Остальные слагаемые тоже делятся на 5, поскольку их коэффициенты делятся на 5. Значит, исходное выражение кратно 5 для всех натуральных n.