Докажите, что функция принимает положительные значения на всей области определения f(x)=5x-4

Я не очень говорю по-украински, хотя немного понимаю. Надеюсь, ты понимаешь по-русски, если нет простить.

Не совсем понятна запись функции, так всегда с корнями. Напишу оба варианта, в зависимости от прочтения.
1. √(2)*x^2+12.
Это типичная квадратичная функция. Коэффициент при x^2 =√(2), что явно больше нуля (значит, ветви параболы направлены вверх), а минимальное значение функция принимает при x=(-b)/(2a)), где b - коэффициент при x, а a - коэффициент при x^2. Итого, функция принимает минимальное значение при 0, а само минимальное значение (подставим 0 вместо x) - это 12.
[12;+∞)
2. Под корнем всё - 2x^2. (√(2x^2)+12)
Тогда можно переформулировать - квадратный корень из квадарата переменной есть модуль (абсолютное значение) переменной (по опр.квадратного.корня: на x возвращается такое неотрицательное y, что y^2=x).
Тогда график - линейная функция под модулем. Минимальное значение модуля любой переменной - 0. Максимум сверху неограничен.
[0;+∞)

X⁶-5x³+4=0
x³=t
t²-5t+4=0
t₁+t₂=5       (-за теормою Виета)
t₁*t₂=4
t₁=4
t₂=1

х³=t
x=∛t
x₁=∛4
x₁≈1.5874
x₂=∛1
x₂=1

x=∛4 и х=1

2*х²- х -3≥ 0


__+____-1____-___1.5____+______>x

x∈(-∞; -1]∪[1.5; +∞)

y=cosx-1
а)  Область определения:   D (cos x-1) = R .
б)  Множество значений:   E (cos x-1 ) = [ – 2 ,  0] 

в)  Четность, нечетность:   функция четная.

г)  Периодичность:   функция периодическая с основным периодом  T = 2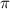 

Точки пересечения с осямии:
ОХ:
cos x -1= 0 
cos x =1

OY:
cos(0)-1=1-1=0

 Промежутки знакопостоянства.:

cosx-1>0  

сosx>1 - не существует, поэтому функция лежит ниже оси ОХ

интервалы возрастания и убывания:

y'=(cosx-1)'= (cosx)'-1'= -sinx

функция возрастает:

-sinx>0

функция убывает:

-sinx<0

Экстремумы: 
(-sinx)'= -cosx
-cos(0)=-1 
-1<0 значит точка x = 0 точка максимума функции