Пусть x,y-два числа, тогда их произведение x*y; а среднее арифметическое их квадратов
получаем неравенство >x*y
x*x+y*y-2xy>0
(x-y)^2>0
что истинно при любых x и y
ЧТД
Пусть x,y-два числа, тогда их произведение x*y; а среднее арифметическое их квадратов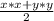
получаем неравенство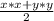 >x*y
>x*y
x*x+y*y-2xy>0
(x-y)^2>0
что истинно при любых x и y
ЧТД