Докажите,что верно равенство:
а)ctg10-tg35-ctg10*tg35=1
б)sin17*sin73-sin21*cos13+sin4*sin86=0

В обоих случаях рассматриваем прямоугольный треугольник с одним из углов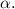

В первом случае примем прилежащий к углу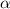  катет за 3, а гипотенузу - за 5. Тогда неизвестный катет вычислим по т. Пифагора как 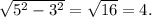Синус угла 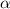есть отношение противолежащего катета к гипотенузе, т.е. 4/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.

Во втором случае примем катет, лежащий против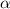 за 4, а гипотенузу - за 5. Неизвестный катет, по теореме Пифагора, будет равен 3. Косинусом 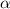есть отношение прилежащего катета к гипотенузе, т.е. 3/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.

Видимо, по условию a + b + c = 1.

Умножим обе части исходного равенства на b:

ab + b² + bc = b. Тогда ab = b - b² - bc и bc = b - b² - ab.

Умножим обе части исходного равенства на c:

ac + bc + c² = c. Тогда ac = c - c² - bc. Рассмотрим чему

тогда равны суммы a + bc, b + ac и c + ab:

a + bc = a + b - b² - ab = (a + b) - b(a + b) = (a + b)(1 - b) =

= (a + b)(a + b + c - b) = (a + b)(a + c).

b + ac = b + c - c² - bc = (b + c) - c(b + c) = (b + c)(1 - c) =

= (b + c)(a + b + c - c) = (b + c)(a + b).

c + ab = c + b - b² - bc = (b + c) - b(b + c) = (b + c)(1 - b) =

= (b + c)(a + b + c - b) = (b + c)(a +c).

Перемножим эти три суммы:

(a + bc)(b + ac)(c + ab) = (a + b)(a + c)(b + c)(a + b)(b + c)(a + c) =

= (a + b)²(a + c)²(b + c)² = ((a + b)(a + c)(b + c))². Это выражение

есть полный квадрат.