Решение 1. Пусть х м/мин - скорость первого мальчика (х – 30) м/мин - скорость второго мальчика 1) 660:2 = 330 (м/мин) - скорость сближения 2)х + х – 30 = 330 2х = 330 + 30 2х = 360 х = 360:2 х = 180 180 м/мин - скорость первого мальчика 3)180 – 30 = 150 (м/мин) - скорость второго мальчика ответ: 180 м/мин ; 150 м/мин. 2. Пусть скорость Бориса х км/ч, а скорость Андрея (х+1) км/ч. Тогда 0,2(х+1) км расстояние, которое Андрей, а (0,2х) км расстояние, которое Борис. Составим уравнение: 0,2(х + 1) + 0,2х = 2 0,2х + 0,2 + 0,2х = 2 0,4х = 1,8 х = 4,5 4,5 км/ч - скорость Бориса Следовательно, 0,2 * 4,5 = 0,9 км - расстояние от дома Бориса при встрече. ответ: 0,9 км
Решение
1. Пусть х м/мин - скорость первого мальчика
(х – 30) м/мин - скорость второго мальчика
1) 660:2 = 330 (м/мин) - скорость сближения
2)х + х – 30 = 330
2х = 330 + 30
2х = 360
х = 360:2
х = 180
180 м/мин - скорость первого мальчика
3)180 – 30 = 150 (м/мин) - скорость второго мальчика
ответ: 180 м/мин ; 150 м/мин.
2.
Пусть скорость Бориса х км/ч, а скорость Андрея (х+1) км/ч.
Тогда 0,2(х+1) км расстояние, которое Андрей,
а (0,2х) км расстояние, которое Борис.
Составим уравнение:
0,2(х + 1) + 0,2х = 2
0,2х + 0,2 + 0,2х = 2
0,4х = 1,8
х = 4,5
4,5 км/ч - скорость Бориса
Следовательно, 0,2 * 4,5 = 0,9 км - расстояние
от дома Бориса при встрече.
ответ: 0,9 км
А1. Разность арифметической прогрессии: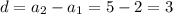
Используем формулу n-го члена арифметической прогрессии:
Число 26 является членом арифметической прогрессии.
Число 30 не является членом арифметической прогрессии, т.к. n ∉ Z
Число 44 является членом этой прогрессии
Число 122 является членом арифметической прогрессии.
ответ: 2) 30.
A2. 1) последовательность чисел, обратных натуральным: -2;-1;1;2
Здесь последовательность не является арифметической прогрессией, так как третий член должен быть 0, а не 1.
2) Нет, это геометрическая прогрессия.
3) 8; 16; 24; ... - арифметическая прогрессия, разность которой d=8
4) 1; 8; 27 - вообще не арифметическая прогрессия.
ответ: 3)
A3. Здесь нужно варианты ответов подставить вместо an.
1) -2 = 1 - n² ⇒ n² = 3 ⇔ n = ±√3 - не является
2) -3 = 1 - n² ⇒ n² = 4 ⇔ n = ±2. Здесь является только при n=2.
3) -4 = 1 - n² ⇒ n² = 5 ⇔ n = ±√5 - не является
4) 3 = 1 - n² ⇒ n² = -2 ⇔ ∅
ответ: 2) -3.
A4. Здесь подходит только an = 2n+6 так как при n=1 имеем a1=8
ответ: 1) an = 2n+6.
B1. Используем формулу n-го члена арифметической прогрессии
С номера n=65 член этой прогрессии больше 260.
C1.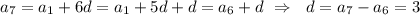
Используем снова формулу n-го члена арифметической прогрессии
n = 56 - номер первого положительного члена этой прогрессии.