Дослідити функцію f(x)=x^3 - 4x на монотонність та - вопрос №341720410 от tatyanafd24 21.01.2022 15:50

Question

Алгебра: Дослідити функцію f(x)=x^3 - 4x на монотонність та екстермуми

tatyanafd24 · Answer

Найдём производную функции, приравняем к нулю, чтобы найти критические(стационарные) точки.

$f'(x)=(x^3-4x)'=3x^2-4\\f'(x)=0\\3x^2-4=0\\x^2=\frac{4}{3}\\x=б\frac{2}{\sqrt{3}}$

Вложение.

Монотонность: $(-\infty;-\frac{2}{\sqrt{3}}]$ - возрастает.

$(-\frac{2}{\sqrt{3}};\frac{2}{\sqrt{3}}]$ - убывает.

$(\frac{2}{\sqrt{3}};+\infty)$ - возрастает.

Экстрэмумы: $-\frac{2}{\sqrt{3}}$ - точка максимума функции.

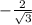$\frac{2}{\sqrt{3}}$ - точка минимума функции.