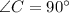Т.к. наибольшего значения в промежутке [1/2; 8] функция достигает при x = 1/2 (по графику и таблице), то подставив это число в функцию, получим её (функции) наибольшее значение:
1/2 = 0,5
0,5 + 16/0,5 = 32,5 --> наибольшее значение функции в промежутке [1/2; 8].
Т.к. наименьшего значения в промежутке [1/2; 8] функция достигает при x = 4 (по графику и таблице), то подставив это число в функцию, получим её (функции) наименьшее значение:
4 + 16/4 = 4 + 4 = 8 --> наименьшее значение функции в промежутке [1/2; 8] (это можно было и в таблице посмотреть).
График и таблица точек прикреплены.
Т.к. наибольшего значения в промежутке [1/2; 8] функция достигает при x = 1/2 (по графику и таблице), то подставив это число в функцию, получим её (функции) наибольшее значение:
1/2 = 0,5
0,5 + 16/0,5 = 32,5 --> наибольшее значение функции в промежутке [1/2; 8].
Т.к. наименьшего значения в промежутке [1/2; 8] функция достигает при x = 4 (по графику и таблице), то подставив это число в функцию, получим её (функции) наименьшее значение:
4 + 16/4 = 4 + 4 = 8 --> наименьшее значение функции в промежутке [1/2; 8] (это можно было и в таблице посмотреть).
НАИБ. 32,5;
НАИМ. 8.
sin (синус) - отношение противолежащего катета к гипотенузе
cos (косинус) - отношение прилежащего катета к гипотенузе
tg (тангенс) - отношение противолежащего катета к прилежащему
ctg (котангенс) - отношение прилежащего катета к противолежащему
arcsin (арксинус) - арксинусом числа х есть значение угла А, для которого sinA=x
arccos (арккосинус) - арккосинусом числа х есть значение угла А, для которого cosA=x
arctg (арктангенс) - арктангенсом числа х есть значение угла А, для которого tgA=x
arcctg (арккотангенс) - арккотангенсом числа х есть значение угла А, для которого ctgA=x
Из ABC
ABC