это Зарание Укажите соответствующий вывод для каждого неравенства. Обоснуйте свой ответ.
а) 5x2- 7x+ 13 ≥0 ;
− x2 + 16x − 64>0;
x2-5x +4≤0;
− x2 + 36<0.
1.Неравенство неимеетрешений.
2.Решением неравенства является вся числовая прямая.
3.Решением неравенства является одна точка.
4.Решением неравенства является закрытый промежуток.
5.Решением неравенства является открытый промежуток.
6.Решением неравенства является объединение двух промежутков. (8б)
2.Решить системунеравенств:
{█(5х^2-16х+11>[email protected]х-18≤0)┤
(5б)
3.Решить неравенство:
(х+4)/(х-9)≤0
4. Решите неравенство (х-5)(2х+4)(2х-8)≤0
ответ: точки экстремума х1 и х2. К точке х2 слева функция возрастает, и вправо от точки х1 функция также возрастает. В промежутке х1 и х2 функция убывает.
Замена: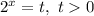
Имеем квадратичную функцию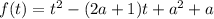 , графиком которой является парабола с ветвями, направленными вверх.
, графиком которой является парабола с ветвями, направленными вверх.
Найдем возможные точки пересечения параболы с осью абсцисс.
Для этого решим квадратное уравнение:
Найдем дискриминант данного уравнения:
Имеем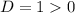 , значит данное уравнение имеет ровно 2 корня:
, значит данное уравнение имеет ровно 2 корня:
Имеем две точки пересечения параболы с осью абсцисс.
Пусть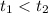 . Тогда
. Тогда 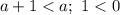 . Имеем неверное неравенство. Следовательно, при всех значениях параметра
. Имеем неверное неравенство. Следовательно, при всех значениях параметра  имеем
имеем 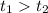 .
.
Тогда квадратичная функция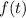 будет меньше 0 при
будет меньше 0 при 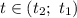
Последнее можно записать так:
Обратная замена:
Если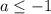 , то имеем:
, то имеем: 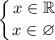
Решением такой системы неравенств является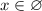
Если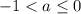 , то имеем:
, то имеем: 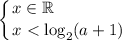
Решением такой системы неравенств является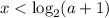
Если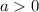 , то имеем:
, то имеем: 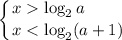
Решением такой системы неравенств является интервал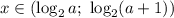
если