Первоначальная функция имеет следующею область определения:
Построим схематично преобразованную функцию Y и наложим ограничение. График функции Y это гипербола, которая лежит в 1 и 3 четвертях относительно следующих прямых: y=0; x=2/3, которые так же являются асимптотами. Пересечение с осями координат:
См. вниз. (1)
Что бы понять как именно убывает функция найдём не сколько точек.
У получившейся кривой есть точка, которая равноудалена от двух асимптот точка A. См. вниз (2)
Найдём координаты этой точки и ещё пару точек кривой, чтобы понять как быстро функция убывает.
4-x²≥0⇒(2-x)(2+x)≥0
x=2 U x=-2
_ + _
-2 2
x∈[-2;2]
2
График во вложении
1)x∈(-∞;0) U (0;∞)
2) (1/7)^-5 < 1; (3,2)^-5 > (3 √2)^-5
3
1)√1-x=3
1-x=9
x=1-9=-8
2)x+2≥0⇒x≥-2 U 3-x≥0⇒x≤3⇒x∈[-2;3]
x+2=3-x
x+x=3-2
2x=1
x=0,5
3)x+1≥0⇒x≥-1
1-x=x²+2x+1
x²+3x=0
x(x+3)=0
x=0
x=-3-не удов усл
4)2x+5≥0⇒x≥-2,5 U x+6≥0⇒x≥-6⇒x≥-2,5
2x+5-2√(2x²+17x+6) +x+6=1
2√(2x²+17x+6)=3x+10
4(2x²+17x+6)=9x²+60x+100
9x²+60x+100-8x²-68x-24=0
x²-8x+76=0
D=64-304=-240<0
нет решения
Первоначальная функция имеет следующею область определения: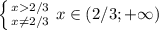
Построим схематично преобразованную функцию Y и наложим ограничение. График функции Y это гипербола, которая лежит в 1 и 3 четвертях относительно следующих прямых: y=0; x=2/3, которые так же являются асимптотами. Пересечение с осями координат: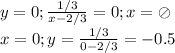
См. вниз. (1)
Что бы понять как именно убывает функция найдём не сколько точек.
У получившейся кривой есть точка, которая равноудалена от двух асимптот точка A. См. вниз (2)
Найдём координаты этой точки и ещё пару точек кривой, чтобы понять как быстро функция убывает.
Существует только x>2/3.
Для ясности нарисую табличку.
См. вниз (3)
Теперь строим график нашей функции.
См. вниз (4)