Формативное оценивание 1) Представьте одночлен в стандартном виде, подчеркнув
его коэффициент.
a) ; b) ; c) ; d) ; k) ;
m)
Образец решения.
2) Найдите значение одночлена:
a) при b) при
c) при d) при
Образец решения.
3) Представьте одночлен в стандартном виде, выпишите его коэффициент и укажите степень одночлена. (Выполнить умножение)
1) 15q∙2p2∙4r5
2) - 2ab33a2b4
3) 52pq2∙ (-4)2qpq
4) 8u44v3∙ (-2) u3
5) 7a∙3b∙4c2
6) -4x5y23xy4
7)-0,45 bс∙ (-1сd) ∙ 9bd
8) 14c3(-5)cd2
9)-0,5 c12(-2)2d18c2
10)0,34 a2x∙ (-1) a3 x2
Образец решения.
15q∙2p2∙4r5=15·2·4·q·p2·r5=120 r5p2q
Коэффициент k=120; степен 1+2+5=8
1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=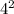 =16 б)у(-3)=
=16 б)у(-3)=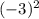 =9 в) у(2)=
=9 в) у(2)=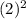 =4
=4
у(3)=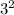 =9 у(-2)=
=9 у(-2)=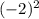 =4 у(-5)=
=4 у(-5)=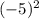 =25
=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.
Кроме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы.
Объяснение:Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.
Задача 1. На складе было 500т угля. Ежедневно стали подвозить по 30т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Решение.
Пусть х – дни, y (тонн) – количество угля на складе. Линейная функция
у = 500 + 30х, где х є N (N- множество натуральных чисел) есть математическая модель ситуации.
При х = 2 имеем у = 500 + 30*2 = 560(т).
При х = 4 имеем у = 500 + 30*4 = 620(т).
При х = 10 имеем у = 500 +30*10 = 800(т).
ответ: 560т; 620т; 800т.
3.2 Использование линейной функции в банковских расчётах.
Задача 2. Вкладчик открыл в банке счёт и положил на него S0 = 150000руб. сроком на 4 года под простые проценты по ставке n = 18% в год. Какой будет сумма S4, которую вкладчик получит при закрытии вклада? На сколько рублей вырастет вклад за p = 4 года. Чему равен коэффициент наращивания?
Решение.
По формуле для простых процентов
SN = SO (1 + np/100) (руб.)
S4 = 150000 (1 + 18*4/100) = 258000(руб.)
258000 – 150000 = 108000(руб.) денежный прирост за 4 года.
S4 : SO = 258000 : 150000 = 1,72 коэффициент наращивания.
ответ: 258000руб.; 108000 руб.; 1,72.