Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что , то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что (при этом подразумевая, что )
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: )
Возможно, это не очень явно, поэтому вспомним, что по предположению , и доделаем:
А это прямо яркий пример противоречия: предположив, что , мы получили .
Из этого следует, что , но и из предположенного же уже следует, что .
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что (при этом )
И тогда уже точно исходя из пунктов 1) и 2), получаем
Используя формулу тангенса суммы аргументов получим:
так как по условию π < α < 3π/ 2, то −1<cosα<0 ⇒ cosα≠0,
мы можем умножить числитель и знаменатель дроби на cosα:
tg(α + π/4) = tg α + tg π/4 / 1 - tg α × tg π/4 = tg α + 1/1 - tg α × 1 = tg α + 1/1 - tg α = sin α/cos α + 1 / 1 - sin α/cos α = sin α + cos α/cos α / cos α - sin α/cos α = sin α + cos α/cos α - sin α
2. Используя основное тождество тригонометрии: sin²α + cos²α = 1 найдем cos α:
sin²α + cos²α = 1 ⇒ cos α = √1 - sin²α
cos α = √1 - (-12/13)² = √1 - 144/169 = √25/169 = 5/13
3) И теперь находим tg(α + π/4) по нахождению про sin α и cos α:
tg(α + π/4) = tg α + tg π/4 / 1 - tg α × tg π/4 = tg α + 1/1 - tg α × 1 = tg α + 1/1 - tg α = sin α/cos α + 1 / 1 - sin α/cos α = sin α + cos α/cos α / cos α - sin α/cos α = sin α + cos α/cos α - sin α = -12/13 + 5/13 / 5/13 - (-12/13) = -7/13 / 5/13 + 12/13 = -7/13 / 17/13 = -7/13 × 13/17 = -7/17
ответ: tg(α + π/4) = -7/17
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что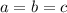 , то есть
, то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что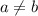 (при этом подразумевая, что
(при этом подразумевая, что 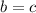 )
)
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: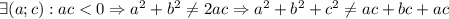 )
)
Возможно, это не очень явно, поэтому вспомним, что по предположению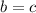 , и доделаем:
, и доделаем:
А это прямо яркий пример противоречия: предположив, что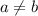 , мы получили
, мы получили 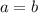 .
.
Из этого следует, что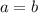 , но и из предположенного же
, но и из предположенного же 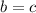 уже следует, что
уже следует, что 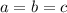 .
.
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что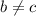 (при этом
(при этом 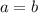 )
)
И тогда уже точно исходя из пунктов 1) и 2), получаем