2. возрастает на всей числовой прямой
Объяснение:
функция вида , где a>0, a≠1 называется показательной
1. a>1 функция возрастающая при х∈(-∞; ∞)
2. 0<a<1 функция убывающая при х∈(-∞; ∞)
, основание а=5, 5>1, => функция возрастает на всей числовой прямой
y=5ˣ
Это показательная функция, она возрастает если основание больше единицы 5 > 1, значит возрастает.
Можно проверить:
x=1 ⇒ y=5; x=2 ⇒ y=25; x=3 ⇒ y=125; x=4 ⇒ y=625; x=5 ⇒ y=3125
ответ: 2) т.к. возрастает на всей области определения, а область определения ни чего не ограничивает.
2. возрастает на всей числовой прямой
Объяснение:
функция вида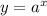 , где a>0, a≠1 называется показательной
, где a>0, a≠1 называется показательной
1. a>1 функция возрастающая при х∈(-∞; ∞)
2. 0<a<1 функция убывающая при х∈(-∞; ∞)
y=5ˣ
Это показательная функция, она возрастает если основание больше единицы 5 > 1, значит возрастает.
Можно проверить:
x=1 ⇒ y=5; x=2 ⇒ y=25; x=3 ⇒ y=125; x=4 ⇒ y=625; x=5 ⇒ y=3125
ответ: 2) т.к. возрастает на всей области определения, а область определения ни чего не ограничивает.