(2x^2-3x+1)(2x^2+5x+1)=9x^2посмотрим что (могу и ошибиться,ибо все делаю не так как надо)1.)приравниваем к нулю: (2x^2-3x+1)(2x^2+5x+1)-9x^2=0 2.) раскрываем скобки: 4x^4 +10x^3+2x^2 -6x^3-15x^2-3x+2x^2+5x+1-9x^2=0 4x^4+4x^3-20x^2+2x=-1 3)выносим за скобки 2x: 2x(2x^3+2x^2-10x+1)=-1 2x=-1, x1=-0,5дальше,продолжаем2x^3+2x^2-10x+1=-1,отсюда 2x^3+2x^2-10x=-2,отсюда 2x за скобки снова: 2x(x^2+x-5)=-2, 2x=-2, x2=-1 x^2+x-5=-1,отсюда x^2+x=4, отсюда x за скобки: x(x+1)=4, x3=4, x4=3x1+x2+x3+x4=-0,5+(-1)+4+3=-1,5+7=5,5
ответ: 25
Объяснение:
Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х=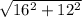 =20
=20
Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.
Используя отношение найдем второй катет большого треугольника через маленькие:
Найдем гипотенузу через формулы площади треугольника.
S=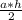 , где а=16+х, h=12
, где а=16+х, h=12
а=16+х-гипотенуза
S=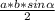 , где sin90=1, а=20, b=15.
, где sin90=1, а=20, b=15.
S=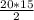 =150
=150
150=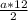 , а=
, а=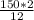 =25.
=25.