Объяснение:
В геометрической прогрессии каждый член, исключая первый, можно найти по формуле:
bn = √(b(n - 1) * b(n + 1)).
Тогда, используя эту формулу, можно найти b9 через данные b8 = 2^(- 12) и b10 = 2^(- 14):
b9 = √(b8 * b10) = √(2^(- 12) * 2^(- 14)) = √(2^(- 26)) = 2^(- 13).
В геометрической прогрессии каждый следующий член можно найти через предыдущий по формуле:
b(n + 1) = bn * q.
Согласно этой формуле:
b9 = b8 * q;
2^(- 13) = 2^(- 12) * q;
q = 2^(- 13)/2^(- 12);
q = 2^(- 1).
Используя формулу нахождения n-го члена геометрической прогрессии через первый член и знаменатель прогрессии bn = b1 * q^(n - 1), получим:
b8 = b1 * q^7;
2^(- 12) = b1 * (2^(- 1))^7;
2^(- 12) = b1 * 2^((- 1) * 7);
2^(- 12) = b1 * 2^(- 7);
b1 = 2^(- 12)/2^(- 7);
b1 = b^(- 5).
Один корень
Левая часть - положительна , значит положительна и правая ,
то есть x > 0 , но тогда функция , стоящая в левой части - возрастает
( как сложная функция , составленная их двух возрастающих ) , а в
правой части - убывающая функция , значит уравнение может иметь не
более одного корня ;
Функция y = непрерывна при x > 0 ;
y ( 0,1 ) = < 0 ; y (1) = ⇒
на интервале ( 0 ; 1 ) y (x) имеет корень и как доказано он
единственный
Объяснение:
В геометрической прогрессии каждый член, исключая первый, можно найти по формуле:
bn = √(b(n - 1) * b(n + 1)).
Тогда, используя эту формулу, можно найти b9 через данные b8 = 2^(- 12) и b10 = 2^(- 14):
b9 = √(b8 * b10) = √(2^(- 12) * 2^(- 14)) = √(2^(- 26)) = 2^(- 13).
В геометрической прогрессии каждый следующий член можно найти через предыдущий по формуле:
b(n + 1) = bn * q.
Согласно этой формуле:
b9 = b8 * q;
2^(- 13) = 2^(- 12) * q;
q = 2^(- 13)/2^(- 12);
q = 2^(- 1).
Используя формулу нахождения n-го члена геометрической прогрессии через первый член и знаменатель прогрессии bn = b1 * q^(n - 1), получим:
b8 = b1 * q^7;
2^(- 12) = b1 * (2^(- 1))^7;
2^(- 12) = b1 * 2^((- 1) * 7);
2^(- 12) = b1 * 2^(- 7);
b1 = 2^(- 12)/2^(- 7);
b1 = b^(- 5).
Один корень
Объяснение:
Левая часть - положительна , значит положительна и правая ,
то есть x > 0 , но тогда функция , стоящая в левой части - возрастает
( как сложная функция , составленная их двух возрастающих ) , а в
правой части - убывающая функция , значит уравнение может иметь не
более одного корня ;
Функция y =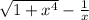 непрерывна при x > 0 ;
непрерывна при x > 0 ;
y ( 0,1 ) =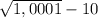 < 0 ; y (1) =
< 0 ; y (1) = 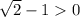 ⇒
⇒
на интервале ( 0 ; 1 ) y (x) имеет корень и как доказано он
единственный