Тангенс наклона касательной, вида y=kx+b, к графику у=f(x), с абсциссой x₀ у точки касания, равен f'(x₀): tgα=k=f'(x₀).
f(x)=2x³-3x²-4; y=12x+1
Прямые вида y=kx+b параллельны, если k - одинаковый коэффициент. Откуда 12=k=f'(x₀).
f'(x) = (2x³)'-(3x²)'-4' = 6x²-6x
f'(x₀) =
Осталось проверить, что y=12x+1 не является касательной к y=f(x) т.к. эта прямая должна быть параллельна касательной, а не совпадать с ней.
12x+1 = 2x³-3x²-4
2x³-3x²-12x-5 = 0
x²(2x+1) - 2x(2x+1) - 5(2x+1) = 0
(2x+1)(x²-2x-5) = 0
x=-0,5 или x²-2x-5=0, D=(-2)²-4·(-5) = 24 > 0 ⇒ уравнение имеет 3 решения, поэтому y=12x+1 не касается y=f(x). В данном случаи при касании было бы 2 решения.
В задаче необходимо найти вероятность события: выпало 6 очков обозначим за A в серии из 4 испытаний не менее 3 раз. Т.е. нужно найти вероятность двух событий выпадения 6 очков в 3-х испытаниях - обозначим как событие B и в 4-х испытаниях - обозначим как событие C серии. Все испытания у нас независимые. Согласно Классического определения вероятности Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта в котором может появиться это событие. В нашем случае всего 6 возможных исходов (6 граней у кубика n=6) и 1 благоприятствующее (m=1), т.е. вероятность события A равна p(A)=m/n=1/6. Для нахождения вероятности наступления события A в серии независимых испытаний применим формулу Бернулли Pn,k=Cknpkqn−k где n - независимые испытания n=6, k - количество наступивших событий (3 или 4 раза выпало 6 очков, т.е. два случая m=3 событие B, m=4 событие C), p - вероятность наступления события A, где p(A)=16, q=1−p=1−16=56 - вероятность противоположного события (т.е. выпало количество очков не равное 6). Подставим в формулу Бернулли P(B)4,3=C34(1/6)3(5/6)4−3=4!3!(4−3)!1/6^3*5^6=20/6^4 P(C)4,4=C44(1/6)^4*(5/6)^4−4=1/6^4 получили две вероятности - наступления событий B и C. Для нахождения вероятности события P(B+C применим теорему сложения вероятностей. Т.к. события не зависимые, то P(B+C)=P(B)+P(C) подставим значения P(B+C)=P(B)4,3+P(C)4,4=20/6^4+1/6^4=21/6^4=6/432=1/72
ответ: вероятность выпадения в серии из 4-х испытаний 6 очков не менее 3-х раз равна P(B+C)=1/72
Тангенс наклона касательной, вида y=kx+b, к графику у=f(x), с абсциссой x₀ у точки касания, равен f'(x₀): tgα=k=f'(x₀).
f(x)=2x³-3x²-4; y=12x+1
Прямые вида y=kx+b параллельны, если k - одинаковый коэффициент. Откуда 12=k=f'(x₀).
f'(x) = (2x³)'-(3x²)'-4' = 6x²-6x
f'(x₀) =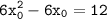
Осталось проверить, что y=12x+1 не является касательной к y=f(x) т.к. эта прямая должна быть параллельна касательной, а не совпадать с ней.
12x+1 = 2x³-3x²-4
2x³-3x²-12x-5 = 0
x²(2x+1) - 2x(2x+1) - 5(2x+1) = 0
(2x+1)(x²-2x-5) = 0
x=-0,5 или x²-2x-5=0, D=(-2)²-4·(-5) = 24 > 0 ⇒ уравнение имеет 3 решения, поэтому y=12x+1 не касается y=f(x). В данном случаи при касании было бы 2 решения.
ответ: х = {-1;2}.
Pn,k=Cknpkqn−k
где n - независимые испытания n=6, k - количество наступивших событий (3 или 4 раза выпало 6 очков, т.е. два случая m=3 событие B, m=4 событие C), p - вероятность наступления события A, где p(A)=16, q=1−p=1−16=56 - вероятность противоположного события (т.е. выпало количество очков не равное 6). Подставим в формулу Бернулли
P(B)4,3=C34(1/6)3(5/6)4−3=4!3!(4−3)!1/6^3*5^6=20/6^4
P(C)4,4=C44(1/6)^4*(5/6)^4−4=1/6^4
получили две вероятности - наступления событий B и C. Для нахождения вероятности события P(B+C применим теорему сложения вероятностей. Т.к. события не зависимые, то
P(B+C)=P(B)+P(C)
подставим значения
P(B+C)=P(B)4,3+P(C)4,4=20/6^4+1/6^4=21/6^4=6/432=1/72
ответ: вероятность выпадения в серии из 4-х испытаний 6 очков не менее 3-х раз равна P(B+C)=1/72