Відповідь:
1. D(f) = R
2. Парність, непарність функції:
f(-x) = 4(-x)^2-(-x)^4 - 3= (x^2-3)(1-x)(1+x) = f(x) функція парна.
3. Нулі функції:
4. f'(x) =
f(x) зростає на ( -∞; -√2] U [0;√2]
f(x) спадає на [-√2; 0] U [√2; +∞)
5. x max = ±√2
x min = 0
f(0) =
f(-√2) =1
f(√2) =1
Пояснення:
Для побудови графіка:
https://math.semestr.ru/math/plot.php
Відповідь:
1. D(f) = R
2. Парність, непарність функції:
f(-x) = 4(-x)^2-(-x)^4 - 3= (x^2-3)(1-x)(1+x) = f(x) функція парна.
3. Нулі функції:
4. f'(x) =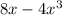
f(x) зростає на ( -∞; -√2] U [0;√2]
f(x) спадає на [-√2; 0] U [√2; +∞)
5. x max = ±√2
x min = 0
f(0) =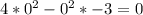
f(-√2) =1
f(√2) =1
Пояснення:
Для побудови графіка:
https://math.semestr.ru/math/plot.php