Данная последовательность не монотонна, так как она знакочередующаяся:
Из этого следует, что
Что нарушает условие монотонности
∀ ∈Ν или
∀ ∈Ν
Используем теорему об ограниченности сходящейся последовательности. Так как при →∞ →0, то последовательность ограничена.
В случае, если теорема не изучалась, можно поступить следующим
Так как ||||, а , то ||, что означает ограниченность последовательности
Данная последовательность не монотонна, так как она знакочередующаяся:
Из этого следует, что
Что нарушает условие монотонности
Используем теорему об ограниченности сходящейся последовательности. Так как при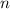 →∞
→∞ 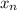 →0, то последовательность ограничена.
→0, то последовательность ограничена.
В случае, если теорема не изучалась, можно поступить следующим
Так как |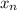 |
|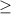 |
|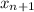 |, а
|, а 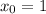 , то |
, то |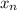 |
|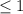 , что означает ограниченность последовательности
, что означает ограниченность последовательности