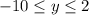Известно, что четверть всех рабочих некоторой отрасли промышленности имеет среднее образование. Для обследования выбрано наудачу 2000 рабочих.
Найти:
1) наивероятнейшее число рабочих со средним образованием;
2) вероятность того, что 1500 рабочих имеют среднее образование;
3) вероятность того, что от 1000 до 1500 рабочих имеют среднее образование.

В решении.

Объяснение:

Побудуйте графік функції у = 3(х – 2)2 за до геометричних перетворень. Підготуйте таблицю значень початкової функції у = х2, вибравши зручні для побудови значення аргументу.

Постройте график функции у = 3(х – 2)² с геометрических преобразований. Подготовьте таблицу значений начальной функции

у = х², выбрав удобные для построения значения аргумента.

График функции у = 3(х – 2)² парабола, получен при сдвиге классической параболы у = х² на две единицы вправо и "уже" её за счёт множителя 3.

Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.

Таблица:

х    0     1      2      3      4

у    12    3     0      3      12

По вычисленным точкам построить параболу.

Таблица значений начальной функции у = х²:

х    -3     -2     -1       0      1      2     3

у     9      4       1       0      1      4     9

Объяснение:

1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.

В примере в) коэффициенты k=5, значит их графики параллельны.

2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.

3. АБВГ

2413

4. 2x + y = 8

2x - y = 1

Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:

2x - (8 - 2x) = 1

2x - 8 + 2x = 1

4x = 9

x = 2,25

y = 8 - 2*2,25 = 8 - 4,5 = 3,5

ответ: (2,25; 3,5)

5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.

2)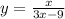 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.

б)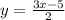 при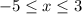

Если x = -5, то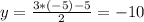

Если х= 3, то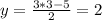

Значит,