Как можно быстрее, . 2. придумайте 2 показательных уравнения, равносильных уравнению: (2 целых 1/3)^x+7 = 9/49 3. log (x^2-6x) по основанию 0,99 > log (6x-35) по основанию 0,99. решить. 4. найдите координаты точек пересечения графиков функций y= log x (по основанию 0,1) и y= корень из трёх x - 1 5. графически решить: (1/2)^2-x ≤ -2x+5 6. решить систему: 5y/x=5/4 √y(x+15) = 2
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство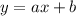
. Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить 
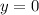. Тогда получим, что 
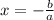, значит пересечение с осью x происходит в точке 
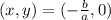. Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.
3*(1-q^n)=1023*(1-q)
q^(n-1)=256
(1-q^n)=341*(1-q) или, что то же самое: (q^n-1)=341*(q-1)
Вероятно, все ж , q -целое, тогда либо q=2 n=9
либо 4 n=5
либо 16 n=3
256 n=2
Легко видеть, что годится только q=4 n=5
ответ: q=4 n=5
б) 243* (3^(-n)+1)=182*(1/3+1)
243*(1-(-3)^(-n))=182*4/3
729 -3^6*(-3)^(-n)==728
(3^6)*(-3)^(-n)=1
ответ:
n=6
an=243*(-1/(3^5))=-1