. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .
Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать
.
. Применим формулу комбинаторики.
Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).
Число сочетаний из n элементов по k элементов обозначается и вычисляется по формуле:
Если я правильно поняла, то нужно заполнить поле y при определенном x. Так и поступим.
Подставляем на место x поочередно числа. Первое уравнение я напишу подробно.
y= -3.1 + (-8.9) x= -8.9
y= -3.1-8.9 (плюс на минус будет минус)
Если только начали работать с минусами то можно их вынести за скобку.
y= -(3,1+8,9)
y= -(12) = -12
При x= -8.9 y=-12
Идем далее. Все делаем по тому же принципу, расписывать я эти выражения не буду.
x=-2.4
y= -3.1+(-2.4)
y= -5.5 При x=-2.4 y=-5.5
x= 1.9
y=-3.1+1.9
y= 1.9-3.1(от перемены мест слагаемых значение суммы не меняется)
y=-1.2 x= 1.9
y= -3.1+7.6
y= 4.5 x=7.6
y=-3.1+12.9
y= 9.8 x= 12.9
Готово. Надеюсь правильно поняла задание. Пс. Это можно было решить и на калькуляторе)
Объяснение:
Задачу можно решить различными .
. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .
Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать
.
. Применим формулу комбинаторики.
Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).
Число сочетаний из n элементов по k элементов обозначается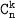
и вычисляется по формуле:
Так как n = 15 и k = 5, то