⦁ Какая из данных последовательностей является геометрической прогрессией?
А) 1; 4; 16; 64; Б) 12; 9; 6; 3; В) 1; 3; 6; 9; Г) -10; -8; -6.
⦁Б) Найдите знаменатель геометрической прогрессии b9 =-250, b^0=50
В). Найдите неизвестные члены геометрической прогрессии b1 ,2; 4; 8; 16; b6
Г)Найдите первый член геометрической прогрессии (bn), если b5 = 36, q= - 2.
Д)Найдите четыре числа, образующих геометрическую прогрессию, у которой первый член больше третьего на 6, а второй – меньше четвертого на 3.
5
Обозначим ширину дорожки как X
Тогда длина бассейна с дорожкой будет 9+2Х
ширина бассейна с дорожкой 6+2Х
Площадь бассейна с дорожкой S=(9+2X)*(6+2X)
54+54=(9+2X)*(6+2X)
Раскроем скобки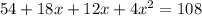
Приведем подобные слагаемые и перенесем 108: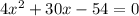
Разделим уравнение на два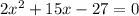
Находим дискриминант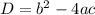
Находим корни уравнения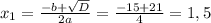
1. Делим на cos^2x
3sin^2x/ cos^2x - 4 sinx/cosx +1 = 0
3tg^2X - 4 tgx +1=0
пусть tgx = t
3t^2-4t+1=D= 16-12=4
t1=4+2/6 = 1
t2 = 4-2/6=1/3
1)tgx=1 2)tgx = 1/3
x = П/4+Пn, nєZ x= arctgx1/3+Пn, nєZ
2. sin²x - 9sinx*cosx+3 cos²x=-sin^2x - cos^2x
sin²x - 9sinx*cosx+3 cos²x+sin^2x + cos^2x=0
2sin²x- 9sinx*cosx+4 cos²x=0 /cos^2x
2th^2x - 9tgx +4=0
tgx=t
2t^2-9t+4=0
D=31-32 =49
t1=4
t2=1/2
1) 2)
tgx=4 tgx=1/2
x=arctg4 +Пn, nєZ x=arctg1/2+Пn, nєZ