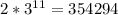-x^3-x^2+16x-20=0⇒x^3+x^2-16x+20=0 Когда уравнение выше второй степени и сразу не видно как разложить на множители, корень уравнения находится подбором среди делителей свободного члена. В данном примере испытываем делители числа 20, например 2: 2^3+2^2-16*2+20=8+4-32+20=0⇒ x=2 - корень уравнения Теперь можно понизить степень уравнения, разделив многочлен на (x-2): x^3+x^2-16x+20=(x-2)(x^2+3x-10) К сожалению, здесь не могу продемонстрировать деление столбиком многочленов (x-2)(x^2+3x-10)=0⇒x^2+3x-10=0 По теореме Виетта x1+x2=-3; x1*x2=-10⇒ x1=-5; x2=2
Аня, Боря и Вася делят 12 различных открыток (возможно совсем несправедливо). Сколько имеется это сделать так, чтобы самая красивая открытка досталась не Васе?
Каждому из вариантов распределения открыток можем сопоставить число записанное в троичной системе счисления (например 0 соответствует Ане, 1 - Боре, 2 - Васе). Всего 12 значных чисел в троичной системе счисления будет
Чтобы самая красивая открытка не досталась Васе (т.е. чтобы в одной позиций 12-значного числа не было цифры 2) вариантов будет
Когда уравнение выше второй степени и сразу не видно как разложить на множители, корень уравнения находится подбором среди делителей свободного члена.
В данном примере испытываем делители числа 20, например 2:
2^3+2^2-16*2+20=8+4-32+20=0⇒
x=2 - корень уравнения
Теперь можно понизить степень уравнения, разделив многочлен на (x-2):
x^3+x^2-16x+20=(x-2)(x^2+3x-10)
К сожалению, здесь не могу продемонстрировать деление столбиком многочленов
(x-2)(x^2+3x-10)=0⇒x^2+3x-10=0
По теореме Виетта
x1+x2=-3; x1*x2=-10⇒
x1=-5; x2=2
Аня, Боря и Вася делят 12 различных открыток (возможно совсем несправедливо). Сколько имеется это сделать так, чтобы самая красивая открытка досталась не Васе?
Каждому из вариантов распределения открыток можем сопоставить число записанное в троичной системе счисления (например 0 соответствует Ане, 1 - Боре, 2 - Васе). Всего 12 значных чисел в троичной системе счисления будет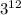
Чтобы самая красивая открытка не досталась Васе (т.е. чтобы в одной позиций 12-значного числа не было цифры 2) вариантов будет