Дробь можно представить в виде конечной только в том случае если в знаменателе есть число кратное только двум ; либо пяти ; либо сразу число одновременно кратное только 5 и 2 (то есть оно кратно 10 ) В остальных случаях если в знаменателе будут числа кратные простым 3 ; 7 ; 11 ; 13 и т.к.д то дробь будет бесконечно периодической Но перед этим важно сократить дробь чтобы числитель ; и знаменатель обязательно были взаимно простыми Перейдем к решению задачи :a) Как видно у дроби знаменатель кратен только пяти ; и поэтому дробь конечна b) Здесь аналогично знаменатель кратен только пяти ; из-за чего дробь конечна r) В этом случае знаменатель одновременно кратен ; и пяти и двум из-за чего дробь конечна g) Можно заметить что у дроби числитель и знаменатель взаимно простые числа ; и также в знаменателе простое число из чего выходит эта дробь является бесконечно периодической ; или же ее нельзя представить в виде конечной
ответ: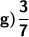
Объяснение:
Дробь можно представить в виде конечной только в том случае если в знаменателе есть число кратное только двум ; либо пяти ; либо сразу число одновременно кратное только 5 и 2 (то есть оно кратно 10 ) В остальных случаях если в знаменателе будут числа кратные простым 3 ; 7 ; 11 ; 13 и т.к.д то дробь будет бесконечно периодической Но перед этим важно сократить дробь чтобы числитель ; и знаменатель обязательно были взаимно простыми Перейдем к решению задачи :a) Как видно у дроби