картинка имеющая форму прямоугольника длина которого 10 см а ширина 15 см, наклеена на лист бумаги так, что обращовалась рамка одинаковой ширины. Определи ширину рамки, если известно что площядь листа бумаги равна 336 см2

Показать ответ

Ответ:

nadj5555

14.10.2021 14:41

1)Докажите нер-во: 1.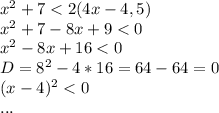 x^2+7

Не знаю, честно говоря что здесь требуется конкретно док-ть, прости. Т.к. тут квадрат меньше 0..

$(2a-5)(2a+5)-(3a-2)^23(4a-9)-2\\4a^2-25-9a^2+12a-412a-27-2\\-5a^2-2912a-29\\-5a^212a /*(-1)\\5a^2$

$2a^2-8a+160 /:2\\a^2-4a+80\\D=16-32=-16\\$

Вот тут могу док-ть и обосновать, т.к. данное квадратное ур-ие - вечный "плюс" и поэтому оно всегда будет больше 0 по определению. Вечный плюс, т.к. его дискриминант меньше 0.

2)Известно, что 7 <a <9. Оцените значение выражений:

1. a-3

2. -5a

$7(-5)*9\\-35(-5a)-45\\or\\-45$

3) Дано 4 <a <3b, 2 <b <3 Оцените значение выражений: 1. а-3b

2. b-4а

3. ab

Не могу подсказать, забыла как это делать:с. Могу до утра еще исправить, если время будет. Условие я правильно записала твоих заданий?

0,0(0 оценок)

Ответ:

nk291726

01.05.2022 13:02

Будем считать, что задание звучит так:

Углы треугольника ABC относятся так: А: В: С=1:2:3.

Сумма углов равна 180 градусов.

Тогда угол А = (180/(1+2+3))*1 = 180/6 = 30 градусов.

Угол В = 30*2 = 60 градусов.

Угол С = 30*3 = 90 градусов.

Далее применяем свойства биссектрисы:

1) она делит угол В пополам, угол АВМ = МВС = 60/2 = 30 градусов.

2) сторона АС точкой Д делится в отношении сторон угла В.

Треугольник АВМ равнобедренный (2 угла по 30 градусов).

Тогда отрезок АМ равен биссектрисе ВМ и равен 4.

В треугольнике МВС искомый отрезок МС лежит в прямоугольном треугольнике против угла 30 градусов, значит, он равен половине гипотенузы ВМ, то есть, МС = 4/2 = 2.

ответ: МС = 2.

0,0(0 оценок)

Популярные вопросы: Алгебра