Дискриминант извлекается из корня и с учетом того, что корни целые, то можно положить a = ±2019 и b = -2 * 2019
Следовательно, - делится на 2019²
Объяснение:
Докажем, что дискриминант этого уравнения делится на 2019².
По формуле Виета:
x₁+x₂= -a/2019
x₁•x₂=b/2019
По условию x₁ и x₂ целые числа, тогда a/2019 и b/2019 целые числа. Поэтому a=2019•c и b=2019•d, c∈Z и d∈Z.
Дискриминант имеет вид:
D=a²-4•2019•b=(2019•c)²-4•2019•(2019•d)=2019²•(c²-4•d)
что и доказывает утверждение.
Дискриминант извлекается из корня и с учетом того, что корни целые, то можно положить a = ±2019 и b = -2 * 2019
Следовательно,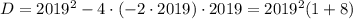 - делится на 2019²
- делится на 2019²
Объяснение:
Докажем, что дискриминант этого уравнения делится на 2019².
По формуле Виета:
x₁+x₂= -a/2019
x₁•x₂=b/2019
По условию x₁ и x₂ целые числа, тогда a/2019 и b/2019 целые числа. Поэтому a=2019•c и b=2019•d, c∈Z и d∈Z.
Дискриминант имеет вид:
D=a²-4•2019•b=(2019•c)²-4•2019•(2019•d)=2019²•(c²-4•d)
что и доказывает утверждение.