Квадратные уравнения. 1. Решите уравнение:
1) 6х2 + 18х = 0.
2) 4х2 – 9 = 0.
3) x2 – 8x + 7 = 0.
4) 3х2 + 5x + 6 = 0.
5) (4х + 3)2 = (2х – 1)2.
6) x2 – 3ах – 4а2 = 0.
2. Один из корней уравнения x2 + 11х + а = 0 равен 3. Найдите другой корень и коэффициент а.
3. Периметр прямоугольника равен 22 см, а его площадь — 24 см2. Найдите длины сторон прямоугольника.
4. Даны четыре последовательных целых числа. Сумма произведений двух крайних и двух средних чисел равна 38. Найдите эти числа.
5. Уравнение x2 + 2х – 3а2 = 0 имеет корни х1 и x2. Напишите квадратное уравнение, корни которого равны х1 – 1 и x2 – 1.
1) а) 11/6 и 12/7
11/6 = 77/42; 12/7 = 72/42
77/42 > 72/42
11/6 > 12/7
б) 0,35 и 2/5 = 0,4
0,35 < 0,4
0,35 < 2/5
2) а) 3,6/4,5*1,6 36/45*16/10 = 4/5*8/5 = 32/25
б) 12 + 0,5*(-4)*3 = 12 - 0,5*4*3 = 12 - 6 = 6
3) Всего 2000 книг, из них 20% учебников. 2000*0.2 = 400 учебников.
12% из этих 400 учебников, то есть 0,12*400 = 48 - по математике.
ответ: 48
4) 16, 17, 24, 25, 33 руб.
Среднее равно (16 + 17 + 24 + 25 + 33)/5 = 115/5 = 23 руб.
Размах: 33 - 16 = 17 руб.
5) Как я понял, цифры после скобок - это степени.
(-0,6)^3 = -0,216
(-0,6)^6 = (-0,216)^2 ≈ 0,045 > 0
Порядок чисел такой: -0,6; (-0,6)^3; (-0,6)^6
6) 90/120*100% = 3/4*100% = 75% стала новая цена от цены.
На 100% - 75% = 25% цена была снижена.
ответ: на 25%
В первом сосуде 25 л воды, а во втором - 45 л. Если первый сосуд долить доверху водой из второго сосуда, то второй сосуд будет наполнен только на треть. Если же второй сосуд долить доверху водой из первого, то первый сосуд будет наполнен водой только на одну пятую. Найдите вместимость каждого сосуда.
Решение
Пусть первый сосуд содержит 25+х воды , а второй 45+у воды.
Тогда если первый сосуд долить доверху(то есть добавить х литров воды ) то второй будет наполнен на треть
45-x=(45+y)/3 ⇔ 135-3x=45+y ⇔ 3x+y=90
Если же во второй сосуд долить у литров воды то в первый будет заполнен на одну пятую
25-у =(25+х)/5 ⇔ 125-5y=25+х ⇔ x+5y=100
Для того чтобы найти переменные х и у решим систему уравнений
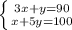
Решаем по методу подстановки.Выразим из первого уравнения переменную y
y= 90-3x
и подставим во второе уравнение
x + 5(90 - 3x) = 100
x + 450 - 15x = 100
-14x = -350
x = 25
y = 90 - 3*25 = 90 - 75 = 15
Следовательно объем первого сосуда равен
25 + х = 25 + 25 = 50 литров
а объем второго сосуда
45 + у = 45 + 15 = 60 литров
Проверка:
Если первый сосуд налить еще 25 литров воды то он будет полным.
Во втором сосуде останется 45-25=20 литров то есть ровно 1/3 от 60 литров.
Если во второй сосуд налить еще 15 литров то он тоже будет полным.
В первом сосуде останется 25-15=10 литров воды = 50/5(или одна пятая от объема сосуда)
ответ: 50 литров, 60 литров